Dérivée
11 messages
- Page 1 sur 1
Dérivée
Bonjour, on me demande d'étudier le signe de variation de cette fonction: f(x)=(racine carré de (x^2+81))/4+(15-x)/6. Je suppose donc qu'il faut calculer la dérivée et trouver ses racines pour voir quand est-ce qu'elle est positive. Or je ne vois pas comment calculer cette dérivée. A-t-on le droit de faire : (u'v-uv')/v^2 + (u'v-uv')/v^2
Re: Dérivée
C'est donc = \dfrac{\sqrt{x^2+81}}{4}+\dfrac{15-x}{6}) , c'est bien ça ?
, c'est bien ça ?
Tu as une somme de 2 fonctions.
La dérivée d'une somme est la somme des dérivées.
Tu as une somme de 2 fonctions.
La dérivée d'une somme est la somme des dérivées.
Re: Dérivée
Tu peux mais dans 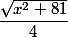 , le 4 est une constante.
, le 4 est une constante.
Tu peux l'écrire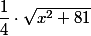
Et la dérivée de k.u, c'est k.u'
Tu peux l'écrire
Et la dérivée de k.u, c'est k.u'
dérivée
Bonjour on me demande de trouver les varitions de f sur l'intervalle (0;15) :
f(x)= (racine carré de( x^2+81))/4 +(15-x)/6
J'ai calculé la dérivée et ca me donne f'(x)=x/(racine carré de (x^2+81)) -1/6 Je n'arrive pas à poursuivre.
On me demande ensuite de déduire x aussi.
Merci d'avance.
f(x)= (racine carré de( x^2+81))/4 +(15-x)/6
J'ai calculé la dérivée et ca me donne f'(x)=x/(racine carré de (x^2+81)) -1/6 Je n'arrive pas à poursuivre.
On me demande ensuite de déduire x aussi.
Merci d'avance.
Re: dérivée
Bonjour,
il faut résoudre f'(x)=0; tu devrais trouver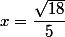
ensuite si tu as oublié comment on fait, tape "tableau de variation " sur le net et tu trouveras plein d'infos te permettant de continuer ton exercice
il faut résoudre f'(x)=0; tu devrais trouver
ensuite si tu as oublié comment on fait, tape "tableau de variation " sur le net et tu trouveras plein d'infos te permettant de continuer ton exercice
Re: dérivée
Ray a écrit:J'ai calculé la dérivée et ca me donne f'(x)=x/(racine carré de (x^2+81)) -1/6 Je n'arrive pas à poursuivre.
Attention, il te manque le facteur
Re: dérivée
Sa Majesté a écrit:Pisigma a écrit:il faut résoudre f'(x)=0; tu devrais trouver
Plutôt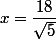
et oui, j'ai mal recopié mon calcul fait sur smartphone!!
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 21 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
