Bonsoir,
Pourriez-vous m'expliquer comment résoudre cet exercice ?
Soit λ ∈ [0,1[ . Montrer qu'il existe un unique n ∈ N* tel que
(n-1)/n <= λ < n/(n+1)
Partie entière
4 messages
- Page 1 sur 1
Re: Partie entière
Eh bien, si tu réalise en plus quel est le premier terme, tu as tout ce qu'il faut pour répondre.
Ou bien, en rapport avec le titre, tu peux raisonner sur le tel que
tel que 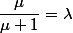 .
.
Ou bien, en rapport avec le titre, tu peux raisonner sur le
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 24 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
