Polynôme et théorème de Rolle

[Matt34200]

Bonsoir j'ai une question à traiter et je bloque un peu sur le " en déduire "
Soit P ∈ R[X]. On suppose que P(a) = P(b) avec a < b. Montrer qu’il existe c ∈]a, b[ tel que
P'(c) = 0. En déduire qu’il existe t ∈]0, 1[ tel que P'((1 − t)a + tb) = 0
Pour la première partie aucun soucis, pour la deuxième je bloque un peu j'ai réussi à montrer l'unicité mais pas l'existence, que faudrait-il faire ?

[perroquet]

Bonjour, matt34200.

Il suffit de montrer qu'il existe tel que , et il n'est pas difficile de voir que convient.

Attention: pour une valeur de donnée, il correspond une unique valeur de . Mais il n'y a pas unicité de et donc pas unicité de .

[Matt34200]

Merci, j'ai rédigé une réponse :
supposons t<1 tel que P'((1-t)a+tb)= 0 on pose alors c = (1-t)a +tb équivalent à c = a -ta +tb equivalent à c = a +t(b-a)
pour t = (c-a)/(b-a) on a bien t<1 car ( c-a)<(b-a) et P'((1-t)a+tb) = P'(c) = 0
c'est bon ?

[perroquet]

Non, la rédaction n'est pas correcte.
Ici, il ne faut pas partir du résultat qui est demandé (en fait, ce serait possible, mais la rédaction serait tellement plus délicate).

Il faut partir du résultat qu'on connaît déjà: il existe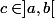 tel que .
Après, on montre qu'il existe tel que . La rédaction qui a été faite pour déterminer l'expression de en fonction de me semble correcte.
Attention, il ne suffit pas de démontrer que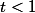 , il faut aussi démontrer que .
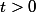Ensuite, en effet, on peut conclure.