DM algèbre L2 maths

[chloe4559]

Bonjour,

je viens vers vous aujourd'hui car je bloque vraiment sur un DM d'algèbre. En effet, je suis bloquée depuis plus d'une semaine....

J'ai un énoncé qui me dit

Soit E un espace vectoriel de dimension n, et φ : E-> E un endomorphisme de E.
1. Montrer que
φ2 = 0 équivalent Im φ C ker φ.
2. On suppose que φ2 = 0.
(a) Déterminer l’ensemble des valeurs propres de φ .
(b) On suppose que φ est diagonalisable. Déterminer φ.
3. On suppose dorénavant que φ2 = 0, et que φ n’est pas diagonalisable.
(a) Montrer que rg(φ) <= n/2. À quelle condition a-t-on Imφ = ker φ ?
(b) Soit F un supplémentaire de ker φ, et (e1, . . . , ep) une base de F.
i. Montrer que (e1, . . . , ep, φ(e1), . . . , φ(ep)) est une famille libre.
ii. Compléter cette famille en une base de E, à l’aide de vecteurs de ker φ (on
précisera bien comment l’on choisit ces vecteurs).
iii. Écrire la matrice de φ dans cette base.

J'ai réussi à trouvé que soit φ admet soit 0 comme valeur propre soit φ n'admet pas de valeur propre.
Dans ce cas, comme on a A=PDP-1 avec D matrice diagonale où les coefficients diagonaux sont les valeurs propres de φ alors D c'est la matrice nulle. Ainsi PDP-1 vaut aussi la matrice nulle et de fait A vaut également la matrice nulle.

Je voulais déjà savoir si ce raisonnement était correct.

Ensuite pour la question 3:
J'ai réussi la question 3)a)
J'ai dit que comme on sait que (e1, . . . , ep) est une base de F en particulier c'est une famille libre et par définition (e1, . . . , ep) est libre si λ1e1+...+λpep=0 implique que λ1=...=λp=0

d'ou φ(λ1e1+...+λpep)= λ1φ(e1)+...+ λpφ(ep)
car φ est linéaire.
D'où λ1φ(e1)+...+ λpφ(ep)=0 équivalent à λ1=...=λp=0
C'es le seul moyen que j'ai trouvé pour montrer que la famille (φ(e1), . . . , φ(ep)) est libre.
Je suis pas sûre que ce soit juste en revanche.
Evidemment les questions d'après je suis encore plus perdue...
Parce que en soit je pourrais faire la question 3b)ii) sans avoir prouvé la question précédente mais je n'y arrive pas du tout...

Est ce que vous pouvez me dire si ce que j'ai fait c'est pas mal où si je suis complètement à côté de la plaque et éventuellement me donner quelques pistes le cas échéant...

Merci d'avance,
Cordialement

[GaBuZoMeu]

Bonjour,

On t'aide déjà ici : https://forums.futura-sciences.com/mathematiques-superieur/894155-exercice-dalgebre-lineaire-deuxieme-annee.html

[chloe4559]

Oui je sais mais justement je n'ai pas trouvé l'aide que j'avais besoin sur ce forum... j'essaye donc ailleurs

[perroquet]

Bonjour, chloe4559.

Sur la question 2a:
Il est exact que si est une valeur propre de , alors .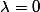
Mais il faut aussi montrer que 0 est une valeur propre de .

Sur la question 2b:
Raisonnement correct, ne pas oublier de préciser que est la matrice de dans une certaine base.

Sur la question 3bi:
L'idée que tu as exposée n'est pas bonne.
Il faut en effet commencer par démontrer que est une famille libre. Pour cela, il faut remarquer que la restriction de à est une bijection de sur (il faut d'abord vérifier que ce résultat est bien dans ton cours).

Sur les questions 3bii et 3biii:
On peut en effet résoudre ces questions en admettant le résultat de la question 3bi.
Mais avant de donner des indications, je vais attendre que les questions précédentes soient résolues.

[chloe4559]

Non il me semble pas qu'il soit dans mon cours.

En revanche, j'ai que (e1,...,ep) est une famille libre cela signifie qu'il existe des λi tels que :
λ1e1+...λpep=0 si et seulement si λ1=...=λp=0

d'autre part dire que (phi(e1),...,phi(ep)) est une famille libre c'est dire que

λ1phi(e1)+...+λpphi(ep)=0 et il faut montrer que λ1=...=λp=0

Comme phi est linéaire, on peut dire que λ1phi(e1)+...+λpphi(ep)=0 est équivalent à

phi(λ1e1)+...+phi(λpep)=0 équivalent à
phi(λ1e1+...λpep)=0

et λ1e1+...λpep par définition de ker phi

et là je suis douteuse sur quelques trucs. Je sens que je suis proche du but !

déjà est ce que je peux dire que si e1,...,ep appartient à F alors λ1e1+...λpep appartient à F ?

[perroquet]

Oui.
Si sont dans , alors, est dans , puisque est un sous-espace vectoriel.

Tu as donc obtenu que est dans . Et comme et sont en somme directe ... tu n'auras pas de mal à conclure.

Il s'agit maintenant de montrer que est une famille libre. On part donc de l'égalité

et il faut établir que les différents coefficients sont nuls.

Un conseil: appliquer à cette égalité.

[perroquet]

Je rappelle que dans la question 2a, il faut montrer que 0 est toujours valeur propre de .

[ijkl]

oui mais elle s'est plantée dès le début de sa réponse

J'ai réussi à trouvé que soit φ admet soit 0 comme valeur propre soit φ n'admet pas de valeur propre

il y aura toujours de(s) valeur(s) propre(s) puisque c'est un endomorphisme

[chloe4559]

Non pour le coup je suis sure de ma réponse. Mon prof m'a dit que mon raisonnement était bon et que 0 était bien la seule valeur propre de phi. Ce que j'ai d'ailleurs prouvé ensuite

[chloe4559]

Oui.
Si sont dans , alors, est dans , puisque est un sous-espace vectoriel.

Tu as donc obtenu que est dans . Et comme et sont en somme directe ... tu n'auras pas de mal à conclure.

Il s'agit maintenant de montrer que est une famille libre. On part donc de l'égalité

et il faut établir que les différents coefficients sont nuls.

Un conseil: appliquer à cette égalité.

Ok bah dans ce cas j'ai déjà fait mon raisonnement car je l'avais fait en attendant votre confirmation pour savoir si Si sont dans , alors, est dans , puisque est un sous-espace vectoriel.
Comme c'est vrai alors mon raisonnement est juste et je peux l'appliquer.

En revanche je pense que je vais m'arrêter la car ca fait plus d'une semaine que je suis dessus et j'ai un peu usé min week end à ce DM et là je bloque vraiment pour la question 3b)iii)

J'ai juste réussi à voir que la dimension de (e1,...,ep,phi(e1),...,phi(ep))=2p et que c'est strictement plus petit que la dimension de E=n car (e1,...,ep,phi(e1),...,phi(ep)) n'est pas encore une base de E puisqu'il faut la compléter.
J'ai donc dit qu'il fallait que 2p+x=n. Ensuite j'ai essayé de passer par les sommes en disant que la somme pour k allant de 1 à p des lambdas(i)ei+ somme pour k allant de 1 à p des lambdas(i)phi(ei) + somme pour k allant de p+1 à n-2p des lambdas(i)e(i)=0 pour prouver qu'on a une famille libre et donc une base par rapport à la dimension mais je n'aboutit à rien...

[ijkl]

oui mais ça je ne dit pas le contraire

moi je vous cite et il y a un truc qui cloche dans la citation

[perroquet]

@ijkl
Il y a des endomorphismes qui n'admettent pas de valeur propre (lorsque le corps de base n'est pas algébriquement clos).

@chloe4559
0 est en effet la seule valeur propre de .
Mais tu as écrit dans ta réponse que pouvait n'avoir aucune valeur propre lorsque . Et ceci est faux.
Si , alors, l'ensemble des valeurs propres de est toujours .

[ijkl]

@ijkl
Il y a des endomorphismes qui n'admettent pas de valeur propre (lorsque le corps de base n'est pas algébriquement clos).

AH mince!!!! j'ai pas fait attention là!!!!!

(c'est pas la première fois mais là je vais m'en rappeler)

Merci

[perroquet]

Sur la question 3bii:
La construction de la base est beaucoup plus simple.
est une famille libre de , on peut la compléter en une base de .
Et est une base de comme réunion de deux bases de deux sous-espaces supplémentaires.

Sur la question 3biii:
elle est assez facile.
Que peut-on dire de la première colonne de cette matrice ?
Que peut-on dire des colonnes d'indices ?

[ijkl]

Mes excuses bien honteuses Cloé

franchement je suis en colère contre moi (une erreur que je me pardonne pas là)