Bonjour,
f(x,y)=sin(x+y)
Je dois donner l'approximation linéaire de f au point (3,-2) et la réponse est 0.54030231*x+0.54030231*y+0.30116867 mais comment faire pour trouver ça ?
Quand j'utilise cette formule je ne trouve pas pareil : f(x,y)=f(x0,y0)+(x-x0,y-y0)gradf(x0,y0)+o(x-x0,y-y0)
merci d'avance
Approximation linéaire
4 messages
- Page 1 sur 1
Re: Approximation linéaire
par mathelot » 20 Nov 2020, 15:11
Bonjour,
posons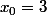
et 
En différentiant:
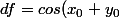(dx+dy))
soit une approximation de l'accroissement de f au voisinage de (x_0;y_0)
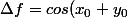(\Delta x+\Delta y))
avec
=sin(x_0+y_0)+cos(x_0+y_0)(x-x_0+y-y_0)+o((x-x_0;y-y_0)))
+cos(1)(-3+2)=0.3011687)
posons
En différentiant:
soit une approximation de l'accroissement de f au voisinage de (x_0;y_0)
avec
Modifié en dernier par mathelot le 20 Nov 2020, 15:25, modifié 2 fois.
Re: Approximation linéaire
par perroquet » 20 Nov 2020, 15:20
(re)Bonjour, w79exz.
En utilisant ta formule, on a:=(3,-2))
= (\cos(x_0+y_0),\cos(x_0+y_0))=(\cos(1),\cos(1)))
L'approximation linéaire de
en )
est donc:
+(x-3)\cos(1)+(y+2)\cos(1)=\cos(1)x+\cos(1)y+\sin(1) -\cos(1))
En utilisant ta formule, on a:
L'approximation linéaire de
Re: Approximation linéaire
par w79exz » 20 Nov 2020, 16:36
Ah ok merci enfaite j'avais mis ma calculette en degré et pas en radian.
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 68 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :