équation complexe avec z^n
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
venusisconfused
- Membre Naturel
- Messages: 26
- Enregistré le: 10 Nov 2020, 16:28
-
 par venusisconfused » 11 Nov 2020, 13:41
par venusisconfused » 11 Nov 2020, 13:41
ijkl a écrit: venusisconfused a écrit: lyceen95 a écrit:Arg(a/b) = Arg(a)-Arg(b)
Pour le 1er exercice, tu devrais 'reconnaître' 2 angles connus.
Désolée, je ne vois pas..
un argument du produit de deux nombre complexes non nuls est la somme des deux arguments de ces deux complexes
ici ce produit est une division donc la somme est une différence
Oui j'ai compris cette partie là mais je ne vois pas quels angles je suis sensée reconnaître, j'imagine que je dois obtenir Arg(3 + racine de 3) - Arg(i + 1) + 2kpi mais ensuite ?
-
venusisconfused
- Membre Naturel
- Messages: 26
- Enregistré le: 10 Nov 2020, 16:28
-
 par venusisconfused » 11 Nov 2020, 13:45
par venusisconfused » 11 Nov 2020, 13:45
lyceen95 a écrit:"étant donné que j'ai à peine mangé depuis 2 jours et que je suis assise à mon bureau pendant des heures, j'ai tendance à faire beaucoup d'erreur d'inattention."
Je n'avais pas vu ce message.
Je vais donc arrêter de te donner des conseils. Tu n'as plus tes facultés mentales. Te donner des conseils pour faire un exercice, ce serait t'envoyer un message ' oui, tu as raison, il faut bosser les maths 24/24, et ça ne sert à rien de faire une pause pour manger'.
C'est ridicule.
Tu vas faire une pause. Quand tu seras suffisamment 'éveillée' pour pouvoir recopier un exercice sans faute dans l'énoncé, alors on pourra recommencer à faire des maths.
Pour l'instant, tu as des difficultés pour recopier un truc, sans réfléchir, et tu crois que tu es en état de faire des exercices de maths ????
Merci pour ton inquiétude mais je vais bien, j'ai fais quelques pauses aujourd'hui et je suis bien réveillée maintenant, quand j'avais posté la question j'étais réveillée depuis plus ou moins 10min donc pas totalement réveillée. C'est pourquoi j'ai mélangé plusieurs énoncés sans faire attention

Mon examen est demain donc j'aurais le temps de me reposer par la suite

-
ijkl
- Membre Relatif
- Messages: 336
- Enregistré le: 28 Sep 2020, 17:43
-
 par ijkl » 11 Nov 2020, 13:47
par ijkl » 11 Nov 2020, 13:47
Lycéen 95 a raison
venusisconfused a écrit: j'ai à peine mangé depuis 2 jours et que je suis assise à mon bureau pendant des heures, j'ai tendance à faire beaucoup d'erreur d'inattention.
vous vous maltraités
est-ce qu'un exo de maths vaut vraiment le coup de mettre en danger sa santé
Je regrette encore une fois de vous avoir paru désagréable
j'ai peur là
-
venusisconfused
- Membre Naturel
- Messages: 26
- Enregistré le: 10 Nov 2020, 16:28
-
 par venusisconfused » 11 Nov 2020, 13:50
par venusisconfused » 11 Nov 2020, 13:50
ijkl a écrit:Lycéen 95 a raison
venusisconfused a écrit: j'ai à peine mangé depuis 2 jours et que je suis assise à mon bureau pendant des heures, j'ai tendance à faire beaucoup d'erreur d'inattention.
vous vous maltraités
est-ce qu'un exo de maths vaut vraiment le coup de mettre en danger sa santé
Je regrette encore une fois de vous avoir paru désagréable
j'ai peur là
Je vais mieux, c'était une exagération de dire que je n'avais rien mangé depuis deux jours, j'avais grignoté quelques trucs que j'avais sous la main et j'ai de quoi boire à coté de moi, quand je sens que j'en fais trop je prendrais une pause mais actuellement je n'estime pas en avoir besoin
-
ijkl
- Membre Relatif
- Messages: 336
- Enregistré le: 28 Sep 2020, 17:43
-
 par ijkl » 11 Nov 2020, 13:57
par ijkl » 11 Nov 2020, 13:57
ah ok! merci de me rassurer
bon alors moi là je me retrouve avec ça
calculer un argument de

en se donnant un entier relatif k
)
est un argument de u
ne le prenez pas mal s'il vous plait mais j'ai un doute sur l'énoncé du 1 vu le contexte de la question
-
venusisconfused
- Membre Naturel
- Messages: 26
- Enregistré le: 10 Nov 2020, 16:28
-
 par venusisconfused » 11 Nov 2020, 14:01
par venusisconfused » 11 Nov 2020, 14:01
ijkl a écrit:ah ok! merci de me rassurer
bon alors moi là je me retrouve avec ça
calculer un argument de

en se donnant un entier relatif k
)
est un argument de u
ne le prenez pas mal s'il vous plait mais j'ai un doute sur l'énoncé du 1 vu le contexte de la question
je pense que je vais abandonner la question 1, cette fois l'énoncé est bien écrit mais il y a sûrement une erreur sur l'exercice en lui même donc je vais simplement passer au deuxième exercice.
Merci beaucoup à vous tous pour votre et désolée pour cette perte de temps du coup, mon prof a souvent tendance à faire des erreurs donc j'aurais dû m'en douter plus tôt que cet exercice étais aussi une erreur.
-
ijkl
- Membre Relatif
- Messages: 336
- Enregistré le: 28 Sep 2020, 17:43
-
 par ijkl » 11 Nov 2020, 14:15
par ijkl » 11 Nov 2020, 14:15
venusisconfused a écrit:
je pense que je vais abandonner la question 1, cette fois l'énoncé est bien écrit mais il y a sûrement une erreur .
...dans le même temps je vois que

est un argument de
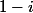
-
ijkl
- Membre Relatif
- Messages: 336
- Enregistré le: 28 Sep 2020, 17:43
-
 par ijkl » 11 Nov 2020, 14:31
par ijkl » 11 Nov 2020, 14:31
je l'ai pas vu facilement mais effectivement

-
ijkl
- Membre Relatif
- Messages: 336
- Enregistré le: 28 Sep 2020, 17:43
-
 par ijkl » 11 Nov 2020, 14:58
par ijkl » 11 Nov 2020, 14:58
edit j'ai oublié

et donc du coup (désolé si je donne la solution mais des fois on est un peu obligé vu le contexte )
}{12n}+2\pi l\right)+ i \times 6^{\dfrac {1}{2n}} \times sin\left(\dfrac {\pi \left(24 k -1\right)}{12n}+2\pi l\right))
avec

et

-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 11 Nov 2020, 16:09
par Pisigma » 11 Nov 2020, 16:09
allez je reviens quand même!!


je crois que le module vous l'avez
quant à l'argument
=\dfrac{\pi}{12}+k\,2\,\pi)
avec

=\dfrac{\pi}{12}+k\,2\,\pi)
=\dfrac{\pi}{12\,n}+\dfrac{k\,2\,\pi}{n})
Modifié en dernier par
Pisigma le 11 Nov 2020, 16:42, modifié 1 fois.
-
ijkl
- Membre Relatif
- Messages: 336
- Enregistré le: 28 Sep 2020, 17:43
-
 par ijkl » 11 Nov 2020, 16:12
par ijkl » 11 Nov 2020, 16:12
Bonjour Pisigma vous parlez du 1)?
on n'a pas le même résultat (en vérifiant pour tout relatif k et tout relatif l et tout naturel non nul n) pourtant j'obtiens bien le résultat attendu
-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 11 Nov 2020, 16:22
par Pisigma » 11 Nov 2020, 16:22
ijkl: je crois que ça vient de ceci
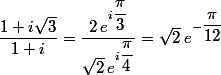
-
ijkl
- Membre Relatif
- Messages: 336
- Enregistré le: 28 Sep 2020, 17:43
-
 par ijkl » 11 Nov 2020, 16:24
par ijkl » 11 Nov 2020, 16:24
Pisigma vous avez essayé ma solution?
elle tombe juste pourtant (ou alors je n'ai pas de contre exemple l'invalidant)
-
ijkl
- Membre Relatif
- Messages: 336
- Enregistré le: 28 Sep 2020, 17:43
-
 par ijkl » 11 Nov 2020, 16:29
par ijkl » 11 Nov 2020, 16:29
pardon Pisigma mais il me semble que ceci est faux
Pisigma a écrit:ijkl: je crois que ça vient de ceci
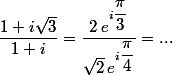
-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 11 Nov 2020, 16:34
par Pisigma » 11 Nov 2020, 16:34
quoi qui est faux?
-
ijkl
- Membre Relatif
- Messages: 336
- Enregistré le: 28 Sep 2020, 17:43
-
 par ijkl » 11 Nov 2020, 16:35
par ijkl » 11 Nov 2020, 16:35
Pisigma a écrit:quoi qui est faux?
je vous cite et il me semble que c'est faux
Pisigma a écrit: 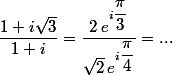
-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 11 Nov 2020, 16:41
par Pisigma » 11 Nov 2020, 16:41
et oui je
traîne une erreur sur mon brouillon
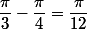
(60°-45°=15° )!!!
j'ai modifié le développement pour le calcul final
-
ijkl
- Membre Relatif
- Messages: 336
- Enregistré le: 28 Sep 2020, 17:43
-
 par ijkl » 11 Nov 2020, 16:44
par ijkl » 11 Nov 2020, 16:44
ok donc la solution est celle-ci (je pense que vous serez d'accord Pisigma
}{12n}+2\pi l\right)+ i \times 6^{\dfrac {1}{2n}} \times sin\left(\dfrac {\pi \left(24 k -1\right)}{12n}+2\pi l\right))
avec

et


Modifié en dernier par
ijkl le 11 Nov 2020, 17:58, modifié 1 fois.
-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 11 Nov 2020, 16:59
par Pisigma » 11 Nov 2020, 16:59
je pense que j'ai mal recopié l'énoncé mon 1er développement était correct
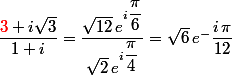
sorry pour le cafouillage
je recopie la bonne solution


je crois que le module vous l'avez
quant à l'argument
=-\dfrac{\pi}{12}+k\,2\,\pi)
avec

=-\dfrac{\pi}{12}+k\,2\,\pi)
=-\dfrac{\pi}{12\,n}+\dfrac{k\,2\,\pi}{n})
-
ijkl
- Membre Relatif
- Messages: 336
- Enregistré le: 28 Sep 2020, 17:43
-
 par ijkl » 11 Nov 2020, 17:04
par ijkl » 11 Nov 2020, 17:04
oui donc on tombe juste (on a le même résultat )
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 30 invités


