équation complexe avec z^n
73 messages
- Page 1 sur 4 - 1, 2, 3, 4
 équation complexe avec z^n
équation complexe avec z^n
Bonjour, j'ai bientôt un examen en algèbre donc je suis en pleine révision et je suis tombée sur deux exercices que je ne comprends pas :
1/ résoudre l'équation suivante : z^n = (3 + i*racine de 3)/(1 + i)
2/ Résoudre dans C* pour n appartenant à N* : [(z + i) / (z - i)]^4 = 1
Merci pour votre aide.
1/ résoudre l'équation suivante : z^n = (3 + i*racine de 3)/(1 + i)
2/ Résoudre dans C* pour n appartenant à N* : [(z + i) / (z - i)]^4 = 1
Merci pour votre aide.
Modifié en dernier par venusisconfused le 11 Nov 2020, 12:17, modifié 2 fois.
Re: équation complexe avec z^n
Bonjour,
1) es-tu sûr du 2d membre car ça donne un argument "inhabituel"
au fait, l'as-tu calculé?
1) es-tu sûr du 2d membre car ça donne un argument "inhabituel"
au fait, l'as-tu calculé?
Re: équation complexe avec z^n
Pisigma a écrit:Bonjour,
1) es-tu sûr du 2d membre car ça donne un argument "inhabituel"
au fait, l'as-tu calculé?
J'ai essayé mais j'en ai déduit que j'avais fait une erreur dans mes calculs ou dans ma méthode car le module était racine de 7 et je ne suis pas sûre de savoir comment calculer l'argument
Re: équation complexe avec z^n
Pour le 2ème exercice, tu as mal recopié.
Tu parles de appartenant à N*, et
appartenant à N*, et  n'apparait plus dans la suite de l'énoncé.
n'apparait plus dans la suite de l'énoncé.
Je vais proposer une piste pour ce que tu as écrit : [(z + i) / (z - i)]^4 = 1
Tu résouds dans un premier temps l'équation Z^4=1 ... il y a 4 racines que tu dois connaître par coeur.
Puis tu te retrouves à devoir résoudre 4 équations relativement simples.
Puis si le vrai énoncé est [(z + i) / (z - i)]^n = 1 ... c'est quasiment la même méthode, avec un peu plus de 'hauteur de vue'.
Tu parles de
Je vais proposer une piste pour ce que tu as écrit : [(z + i) / (z - i)]^4 = 1
Tu résouds dans un premier temps l'équation Z^4=1 ... il y a 4 racines que tu dois connaître par coeur.
Puis tu te retrouves à devoir résoudre 4 équations relativement simples.
Puis si le vrai énoncé est [(z + i) / (z - i)]^n = 1 ... c'est quasiment la même méthode, avec un peu plus de 'hauteur de vue'.
Re: équation complexe avec z^n
lyceen95 a écrit:Pour le 2ème exercice, tu as mal recopié.
Tu parles deappartenant à N*, et
n'apparait plus dans la suite de l'énoncé.
Je vais proposer une piste pour ce que tu as écrit : [(z + i) / (z - i)]^4 = 1
Tu résouds dans un premier temps l'équation Z^4=1 ... il y a 4 racines que tu dois connaître par coeur.
Puis tu te retrouves à devoir résoudre 4 équations relativement simples.
Puis si le vrai énoncé est [(z + i) / (z - i)]^n = 1 ... c'est quasiment la même méthode, avec un peu plus de 'hauteur de vue'.
Effectivement, le n n'apparaît plus dans la suite mais c'est bien comme ça qu'est rédigé l'énoncé, peut-être une erreur ?
Mais merci beaucoup pour ton aide, j'essayerais de faire l'exercice avec tes indications
Re: équation complexe avec z^n
pour le 1 il y a sûrement une erreur dans le second membre revérifie le
Re: équation complexe avec z^n
Pisigma a écrit:pour le 1 il y a sûrement une erreur dans le second membre revérifie le
Pourtant c'est bien l'énoncé
Re: équation complexe avec z^n
j'en doute, mais quel calcul as-tu effectué pour le trouver? et combien as-tu trouvé?
qu'as-tu trouvé comme 2d membre?
qu'as-tu trouvé comme 2d membre?
Re: équation complexe avec z^n
Pisigma a écrit:j'en doute, mais quel calcul as-tu effectué pour le trouver? et combien as-tu trouvé?
Je n'ai pas réussi à faire l'exercice justement, j'essaie de joindre une photo de l'énoncé mais le site ne me laisse pas.. Il s'avère que je me suis effectivement trompée
 ce n'est pas racine de 5 mais plutôt racine de 3
ce n'est pas racine de 5 mais plutôt racine de 3Re: équation complexe avec z^n
Bonjour
on remarquera que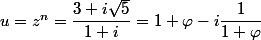
avec le nombre d'or
le nombre d'or
les calculs avec le nombre d'or sont plus sympas à faire qu'avec l'horrible fraction donnée comme ça non?
on remarquera que
avec
les calculs avec le nombre d'or sont plus sympas à faire qu'avec l'horrible fraction donnée comme ça non?
Re: équation complexe avec z^n
venusisconfused a écrit:Pisigma a écrit:j'en doute, mais quel calcul as-tu effectué pour le trouver? et combien as-tu trouvé?
Je n'ai pas réussi à faire l'exercice justement, j'essaie de joindre une photo de l'énoncé mais le site ne me laisse pas.. Il s'avère que je me suis effectivement trompéece n'est pas racine de 5 mais plutôt racine de 3
donc maintenant c'est plus simple, vas-y
Re: équation complexe avec z^n
au fait 
ijkl a écrit:Bonjour
on remarquera que
avecle nombre d'or
les calculs avec le nombre d'or sont plus sympas à faire qu'avec l'horrible fraction donnée comme ça non?
Re: équation complexe avec z^n
Pisigma a écrit:venusisconfused a écrit:Pisigma a écrit:j'en doute, mais quel calcul as-tu effectué pour le trouver? et combien as-tu trouvé?
Je n'ai pas réussi à faire l'exercice justement, j'essaie de joindre une photo de l'énoncé mais le site ne me laisse pas.. Il s'avère que je me suis effectivement trompéece n'est pas racine de 5 mais plutôt racine de 3
donc maintenant c'est plus simple, vas-y
je n'y arrive toujours pas

Re: équation complexe avec z^n
Bonjour,
z^n = (3 + i*racine de 5)/(1 + i)
(3 + i*racine de 5)/(1 + i) = V14 * (3/V14 + i*(V(5/14)) / (V2 * (1/V2 + i*1/V2))
|z^n| = V(7)
arg(z^n) = arctan((V5)/3) - Pi/4
z^n = V(7) * e^(i * (arctan((V5)/3) - Pi/4 + 2k.Pi))
z = 7^(1/(2n)) * e^(i * ((arctan((V5)/3) - Pi/4)/n + 2k.Pi/n) ... avec k entier de 0 à n-1
z0 = 7^(1/(2n)) * e^(i * ((arctan((V5)/3) - Pi/4)/n)
z1 = 7^(1/(2n)) * e^(i * ((arctan((V5)/3) - Pi/4)/n + 2.Pi/n)
...
z(n-1) = 7^(1/(2n)) * e^(i * ((arctan((V5)/3) - Pi/4)/n + 2(n-1).Pi/n)

Edit:
Pas vu le massage avec le nombre d'or avant d'envoyer ...
Mais la résolution que j'ai donnée doit être correcte.
z^n = (3 + i*racine de 5)/(1 + i)
(3 + i*racine de 5)/(1 + i) = V14 * (3/V14 + i*(V(5/14)) / (V2 * (1/V2 + i*1/V2))
|z^n| = V(7)
arg(z^n) = arctan((V5)/3) - Pi/4
z^n = V(7) * e^(i * (arctan((V5)/3) - Pi/4 + 2k.Pi))
z = 7^(1/(2n)) * e^(i * ((arctan((V5)/3) - Pi/4)/n + 2k.Pi/n) ... avec k entier de 0 à n-1
z0 = 7^(1/(2n)) * e^(i * ((arctan((V5)/3) - Pi/4)/n)
z1 = 7^(1/(2n)) * e^(i * ((arctan((V5)/3) - Pi/4)/n + 2.Pi/n)
...
z(n-1) = 7^(1/(2n)) * e^(i * ((arctan((V5)/3) - Pi/4)/n + 2(n-1).Pi/n)
Edit:
Pas vu le massage avec le nombre d'or avant d'envoyer ...
Mais la résolution que j'ai donnée doit être correcte.
Modifié en dernier par Black Jack le 11 Nov 2020, 12:02, modifié 1 fois.
Re: équation complexe avec z^n
commence par rationnaliser ton second membre et cherche le module et un argument du 2d membre
Re: équation complexe avec z^n
ijkl a écrit:Bonjour
on remarquera que
avecle nombre d'or
les calculs avec le nombre d'or sont plus sympas à faire qu'avec l'horrible fraction donnée comme ça non?
je ne gère pas du tout le nombre d'or


Re: équation complexe avec z^n
Salut Black Jack,
comme je vois que tu t'es intercalé dans l'échange bye!
ça semble être l'usage dans Maths-Forum
comme je vois que tu t'es intercalé dans l'échange bye!
ça semble être l'usage dans Maths-Forum
Modifié en dernier par Pisigma le 11 Nov 2020, 12:04, modifié 1 fois.
Re: équation complexe avec z^n
Black Jack a écrit:Bonjour,
z^n = (3 + i*racine de 5)/(1 + i)
(3 + i*racine de 5)/(1 + i) = V14 * (3/V14 + i*(V(5/14)) / (V2 * (1/V2 + i*1/V2))
|z^n| = V(7)
arg(z^n) = arctan((V5)/3) - Pi/4
z^n = V(7) * e^(i * (arctan((V5)/3) - Pi/4 + 2k.Pi))
z = 7^(1/(2n)) * e^(i * ((arctan((V5)/3) - Pi/4)/n + 2k.Pi/n) ... avec k entier de 0 à n-1
z0 = 7^(1/(2n)) * e^(i * ((arctan((V5)/3) - Pi/4)/n)
z1 = 7^(1/(2n)) * e^(i * ((arctan((V5)/3) - Pi/4)/n + 2.Pi/n)
...
z(n-1) = 7^(1/(2n)) * e^(i * ((arctan((V5)/3) - Pi/4)/n + 2(n-1).Pi/n)
bonjour,
j'avais fais une erreur dans l'énoncé, c'était racine de 3 et non 5
 mais merci beaucoup
mais merci beaucoupRe: équation complexe avec z^n
Pisigma a écrit:commence par rationnaliser ton second membre et cherche le module et un argument du 2d membre
j'ai mis le 2nd membre sous forme a + ib et comme module j'ai trouvé racine de 6 mais je n'arrive pas à trouver l'argument...
73 messages
- Page 1 sur 4 - 1, 2, 3, 4
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 26 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
