Salut à tous :
Je vous propose un exercice sur le produit scalaire. Je l'ai déjà travaillé mais je ne suis pas certain des résultats . La 2ème question me pose un problème :
L'unité de mesure des longueurs dans le plan Pest le centimetre. Soit ABCD un rectangle de centre O et tels que : AB=6 a AD= 4 On désigne par le barycentre des points ponderes (A,4) (8,5)
/ Montrer que les vecteurs Ci et DB sont orthogonaux.
2/ Le cercle de centre Cet passant par B recoupe la droite (BD) en J. Calculer DJ .DB(vecteurs) En déduire la valeur de DJ.
3/ Soit □={MeP/ MD^2-MB^2=k}.ou k est un réel donné Prouver que □est une droite puis déterminer la valeur de k pour que soit la médiatrice [BJ)
. Soit r= {Me P/ 13(MD ^2+MJ^2)=178).
Montrer que r un cercle qui passe par O. 5/ Déterminer l'ensemble (E)={MeP/ 4MA^2 +5MB^2 -9MI JI (vecteurs)= 80}
Produit scalaire
5 messages
- Page 1 sur 1
Re: Produit scalaire
2) Un calcul qui ne passe sans doute pas par le chemin attendu :
 représente la puissance du point D par rapport au cercle de centre C et de rayon BC
représente la puissance du point D par rapport au cercle de centre C et de rayon BC
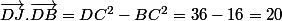
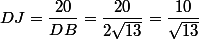
Re: Produit scalaire
Merci pour cette solution mais comment démontrer que (vecteurs)DJ.DB=DC^2-BC^2
La puissance d'un point par rapport à un cercle ne fait pas partie du programme
La puissance d'un point par rapport à un cercle ne fait pas partie du programme
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 69 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
