U sous groupe de (C*,x)

[khâmy]

Bonsoir, je dois vérifier que U (ensemble des modules de z qui vaut 1) est un sous groupe de (C*,x).
J'ai commencé par la caractérisation en disant que U est inclus dans C* et que le neutre de (C*,x) est 1 et qu'il se trouve dans U. Par contre, je ne suis pas du tout sûre pour la suite où j'ai écris que :
Soient z',z dans U:
(le module de z')x(le module de z^-1) = 1 qui appartient à U et ainsi z'xz^-1 appartient à U.

J'aimerais beaucoup avoir de l'aide. Merci d'avance !^^

[GaBuZoMeu]

Bonsoir,

Qu'est-ce qui te pose question, en fait ?

[hdci]

Le raisonnement est bon. Pour démontrer que est un sous groupe du groupe , il suffit de montrer que 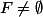et et c'est ce que vous avez fait, sauf peut-être la précision manquante

Attention au phrasé, U n'est pas "l'ensemble de module de z qui vaut 1", mais "l'ensemble des z de module 1"

[khâmy]

Bonsoir,

Qu'est-ce qui te pose question, en fait ?

Ce qui me pose question c'est comme je veux démontrer que z'xz^-1 appartient à U mais comme je pars du module de z'xz^-1, et que je trouve que celui-ci appartient à U, on ne peut pas dire que z'xz^-1 appartient à U, vu que c'est le module et non ce que je cherche à démontrer. Je ne sais pas si je me suis bien exprimée, excusez-moi

[khâmy]

Le raisonnement est bon. Pour démontrer que est un sous groupe du groupe , il suffit de montrer que et et c'est ce que vous avez fait, sauf peut-être la précision manquante

Attention au phrasé, U n'est pas "l'ensemble de module de z qui vaut 1", mais "l'ensemble des z de module 1"

Merci beaucoup !

[capitaine nuggets]

Salut !

Autre méthode, voir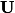 comme le noyau du morphisme de groupes 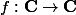défini par .

[GaBuZoMeu]

[
Ce qui me pose question c'est comme je veux démontrer que z'xz^-1 appartient à U mais comme je pars du module de z'xz^-1, et que je trouve que celui-ci appartient à U, on ne peut pas dire que z'xz^-1 appartient à U, vu que c'est le module et non ce que je cherche à démontrer. Je ne sais pas si je me suis bien exprimée, excusez-moi

Pas trop, non. Et j'ai l'impression que tu n'as pas non plus une vision très claire du raisonnement.
est l'ensemble des nombres complexes de module 1.
Hypothèse : et . Ceci veut dire et .
On en déduit , ce qui veut dire .