Convergence série

[MedPr]

Bonjour, voilà l’énoncé d’un de mes exercices la série de terme général converge t-elle ?

Un= 1/2*[ln (n)]^2

J’ai essayé plus méthode :

- le critère de d’Alembert mais cela n’est pas très pertinent

- le critère des équivalents mais je n’arrive pas à trouver un équivalent

Si vous avez d’autres méthodes je suis preneur merci !

[hdci]

Bonjour,
Peut-être qu'en comparant avec une autre série dont on maîtrise mieux le terme général ?

Par exemple, que peut-on dire de par rapport à ?

[MedPr]

On peut dire que (ln n)^2 >> n

[hdci]

Ah ? Pourquoi ?

[MedPr]

Ou plutôt Vu que ln n < n alors (ln 2)^n < n*ln n

[hdci]

Le logarithme de n est supérieur à n ? Il faut revoir le cours !

[phyelec]

Bonjour,

Peut-être une piste voici :

soit

[hdci]

Questions :
1) Quelle est la limite suivante ?


2) En déduire la limite suivante


3) En déduire une comparaison de et de 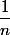("à partir d'un certain " bien sûr)

4) Que sait-on de la série de terme général ?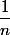

5) Conclure.

Si les limites des fractions avec logarithmes n'ont pas été vues (mais il me semble que c'est fait en terminale ?) :

1) Etudier les variations de la fonction
2) Calculer
3) En déduire la comparaison entre et de 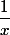"à partir d'un certain ", puis comme la question 3 précédente
4) Comme les questions 4 et 5 précédentes.