Bonjour, Je sollicite votre aide parceque je bloque sur la question 1)b) de mon Dm que voici :
1)a)(résolu) : Résoudre l'équation d'inconnue z complexe z^5=1
Je l'ai résolu grâce à la formule de mon cours mais je ne sais pas comment résoudre le 1)b) :
- En déduire, sous forme de tangente, les solutions de l'équation suivante d'inconnue z complexe :
(1+iz)^5=(1-iz)^5
Je sais que : tan(x) =sin(x) /cos(x) mais je n'ai pas trouvé d'autres pistes de résolution
Merci d'avance pour votre aide !
Question racines cinquièmes de l'unité/tangeantes
6 messages
- Page 1 sur 1
Re: Question racines cinquièmes de l'unité/tangeantes
Bonjour,
Et su tu mets ton équation sous le forme^5= 1) , ça t'aide ?
, ça t'aide ?
Et su tu mets ton équation sous le forme
Re: Question racines cinquièmes de l'unité/tangeantes
Je suis arrivé à mettre l'équation sous cette forme-là, mais je ne vois toujours pas comment faire la suite.
Je pense qu'il faut le mettre sous la forme de la racine cinquième de l'unité mais je ne vois pas comment le mettre ensuite sous la forme de la tangente.
Je pense qu'il faut le mettre sous la forme de la racine cinquième de l'unité mais je ne vois pas comment le mettre ensuite sous la forme de la tangente.
Re: Question racines cinquièmes de l'unité/tangeantes
Bonsoir, au final je trouve :
z=[-i(α-1)]/1+α
Je ne sais pas ensuite comment procéder pour le mettre sous la forme d'une tangente
(désolé je n'ai pas réussi à me servir de l'éditeur d'équation malgré moi)
z=[-i(α-1)]/1+α
Je ne sais pas ensuite comment procéder pour le mettre sous la forme d'une tangente
(désolé je n'ai pas réussi à me servir de l'éditeur d'équation malgré moi)
Re: Question racines cinquièmes de l'unité/tangeantes
Tu as sans doute l'expression des racines 5e de l'unité sous forme 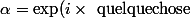) ?
?
Par ailleurs, tu sais sans doute comment s'expriment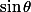 et
et 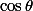 en fonction de
en fonction de 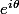 et
et 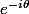 ?
?
Par ailleurs, tu sais sans doute comment s'expriment
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 13 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
