1ere S : Symétries et translations de fonctions
24 messages
- Page 1 sur 2 - 1, 2
1ere S : Symétries et translations de fonctions
Bonjour, je suis en 1ere S et j'ai un DM de maths à faire où je bloque sur quelques questions.
1) Démontrer que la courbe C d'équation y=racine carrée(|x+1|+|x-1|) admet un axe de symétrie.
J'ai calculé f(-x) = racine(|(-x)+1|+|(-x)-1|) = f(x)
Donc la fonction est paire est elle admet un axe de symétrie qui est l'axe des ordonnées.
Ca me parait un peu trop simple pour un DM.
2)Le plan est muni d'un repère orthonormé.
1.Tracer les courbes Cf et Cg des fonctions f et g telles que f(x)=2+1/(x+3) et g(x)= -3-1/(2-x).
2. Determiner les fonctions f°g et g°f en précisant leurs ensembles de définition.
f°g = -x D=R
g°f = x D=R
Voilà ce que j'ai trouvé mais je ne suis pas sure du tout. :triste:
3.Tracer la droite d'équation y =x
4.Soit P et Q les points de coordonnées (alpha ; bêta) et (bêta ; alpha).
Montrer que P et Q sont symétriques par rapport à y=x.
Je n'ai rien trouvé. :mur:
5. Montrer que Cf et Cg sont symétriques par raport à y=x.
Je n'ai rien trouvé non plus. :mur:
Tout aide sera la bienvenue...
Merci d'avance
1) Démontrer que la courbe C d'équation y=racine carrée(|x+1|+|x-1|) admet un axe de symétrie.
J'ai calculé f(-x) = racine(|(-x)+1|+|(-x)-1|) = f(x)
Donc la fonction est paire est elle admet un axe de symétrie qui est l'axe des ordonnées.
Ca me parait un peu trop simple pour un DM.
2)Le plan est muni d'un repère orthonormé.
1.Tracer les courbes Cf et Cg des fonctions f et g telles que f(x)=2+1/(x+3) et g(x)= -3-1/(2-x).
2. Determiner les fonctions f°g et g°f en précisant leurs ensembles de définition.
f°g = -x D=R
g°f = x D=R
Voilà ce que j'ai trouvé mais je ne suis pas sure du tout. :triste:
3.Tracer la droite d'équation y =x
4.Soit P et Q les points de coordonnées (alpha ; bêta) et (bêta ; alpha).
Montrer que P et Q sont symétriques par rapport à y=x.
Je n'ai rien trouvé. :mur:
5. Montrer que Cf et Cg sont symétriques par raport à y=x.
Je n'ai rien trouvé non plus. :mur:
Tout aide sera la bienvenue...
Merci d'avance
Bon allons-y avec tous les détails . On considère deux points A(a,b) et B(b,a) et on veut montrer que A et B sont symétriques par rapport à (D):y=x .
1°) Si a=b alors A(a,a)=B(a,a) sont sur (D) donc symétriques par rapport à (D) .
2°) Si a et b sont distincts alors A et B aussi .
M(x,y) appartient à la médiatrice de [AB] ssi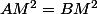
M(x,y) appartient à la médiatrice de [AB] ssi^2+(y-b)^2=(x-b)^2+(y-a)^2)
M(x,y) appartient à la médiatrice de [AB] ssi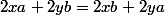
M(x,y) appartient à la médiatrice de [AB] ssi(a-b)=0)
M(x,y) appartient à la médiatrice de [AB] ssi
M(x,y) appartient à la médiatrice de [AB] ssi)
Donc (D) est la médiatrice de [AB] .
Imod
1°) Si a=b alors A(a,a)=B(a,a) sont sur (D) donc symétriques par rapport à (D) .
2°) Si a et b sont distincts alors A et B aussi .
M(x,y) appartient à la médiatrice de [AB] ssi
M(x,y) appartient à la médiatrice de [AB] ssi
M(x,y) appartient à la médiatrice de [AB] ssi
M(x,y) appartient à la médiatrice de [AB] ssi
M(x,y) appartient à la médiatrice de [AB] ssi
M(x,y) appartient à la médiatrice de [AB] ssi
Donc (D) est la médiatrice de [AB] .
Imod
Imod a écrit:Bon allons-y avec tous les détails . On considère deux points A(a,b) et B(b,a) et on veut montrer que A et B sont symétriques par rapport à (D):y=x .
1°) Si a=b alors A(a,a)=B(a,a) sont sur (D) donc symétriques par rapport à (D) .
2°) Si a et b sont distincts alors A et B aussi .
M(x,y) appartient à la médiatrice de [AB] ssi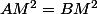
M(x,y) appartient à la médiatrice de [AB] ssi
J'ai compris jusque là, et après tu développe mais moi je trouve :
-2ax-2by=-2bx-2ay
et je ne comprend pas comment tu trouves
ni
stef a écrit:J'ai compris jusque là, et après tu développe mais moi je trouve :
-2ax-2by=-2bx-2ay
Moi aussi mais en multipliant chaque membre par -1 on se débarasse des - .
stef a écrit:et je ne comprend pas comment tu trouves
ni
2ax-2by=2bx-2ay -> 2ax-2bx+2ay-2by=0 -> 2x(a-b)+2y(a-b)=0 -> 2(a-b)(x-y)=0 . Comme 2 et a-b sont non nuls x-y=0 .
Imod
gbsatti a écrit:J'ai l'impression qu'on est dans la meme classe :id: le même DM que moi :we: A ce que je vois c'est deja developpé profitons en :petard:.
Tu dois etre en 1ereS2 du lycee kleber a strasbourg je me trompe ? :lol2:
:++: Oui, t'es qui? si t'es la c'est que t'étais dans la même galère que moi. :lol3:
24 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 69 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
