Norme opérateur
39 messages
- Page 2 sur 2 - 1, 2
Re: Norme opérateur
L'objectif était de calculer  . On n'y est pas encore, mais on a progressé.
. On n'y est pas encore, mais on a progressé.
Peux-tu trouver une suite_n) non nulle telle que
non nulle telle que _n)=(x_n)_n) ? Ça permettrait de conclure.
? Ça permettrait de conclure.
Peux-tu trouver une suite
Re: Norme opérateur
Ah oui ce que vous voulez dire c'est qu'il faut avant de calculer 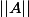 montrer que
montrer que 
Il faut que je trouve une suite tel que :
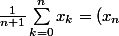_n)
Avec une suite constance cela ne marche pas, je ne vois pas quelle suite_n)
Il faut que je trouve une suite tel que :
Avec une suite constance cela ne marche pas, je ne vois pas quelle suite
Re: Norme opérateur
Non, ce n'est pas ce que je veux dire. Ce que je veux dire, c'est qu'on a montré  . Et que si on trouve une suite
. Et que si on trouve une suite _n) non nulle telle que
non nulle telle que =\mathbf x) , alors on a aussi
, alors on a aussi  .
.
Qu'est-ce qui ne marche pas avec une suite constante ? Au risque de radoter : plus de soin !!
Qu'est-ce qui ne marche pas avec une suite constante ? Au risque de radoter : plus de soin !!
Re: Norme opérateur
Ah et donc si on a  et
et  ça veut dire que
ça veut dire que 
Oui je m'excuse j'essaye de faire de mon mieux mais c'est un cours encore très vague pour moi ...
Si je prends une suite constante différente de 0 par exemple_n=1) alors :
alors :
_n) = (y_n)_n = \frac{1}{n+1} \sum_{k=0}^{n}{x_k} = \frac{1}{n+1} \sum_{k=0}^{n}{1}=\frac{1}{n+1}( n+1 )=1)
ah cela marche alors ...
Oui je m'excuse j'essaye de faire de mon mieux mais c'est un cours encore très vague pour moi ...
Si je prends une suite constante différente de 0 par exemple
ah cela marche alors ...
Re: Norme opérateur
Bon, tu as vu quelque chose.
Mais il y a toujours à redire ! Regarde ton égalité :_n = \dfrac1{n+1}\sum_{k=0}^n 1)
À gauche tu as une suite de nombres réels. À droite tu as un nombre réel. Un nombre réel, ce n'est pas la même chose qu'une suite de nombres réels. Tu écris une égalité entre deux objets qui ne sont pas du même type. Ça amène inévitablement à des confusions et à des erreurs.
Ce qui est correct, c'est :
pour tout entier ,
, 
Là, on écrit des égalités entre objets de type "nombres réels".
Si tu fais de la programmation, tu devrais savoir que faire des confusions sur les types des objets peut causer de graves ennuis.
Mais il y a toujours à redire ! Regarde ton égalité :
À gauche tu as une suite de nombres réels. À droite tu as un nombre réel. Un nombre réel, ce n'est pas la même chose qu'une suite de nombres réels. Tu écris une égalité entre deux objets qui ne sont pas du même type. Ça amène inévitablement à des confusions et à des erreurs.
Ce qui est correct, c'est :
pour tout entier
Là, on écrit des égalités entre objets de type "nombres réels".
Si tu fais de la programmation, tu devrais savoir que faire des confusions sur les types des objets peut causer de graves ennuis.
Re: Norme opérateur
Oui c'est vrai je manque de rigueur et je vous remercie de me reprendre et de me corriger pour que je m'améliore sur ce point là !
Par conséquent on a que pour tout entier n,
Donc on a trouvé une suite non nulle_x=1) tel que
tel que =x_n) c'est à dire tel que
c'est à dire tel que _n=(x_n)_n)
Mais je ne vois pas en quoi ça veut dire que |
------------------------------------------
Update:
Si je reprends la définition de_n||}{||(x_n)_n||} \right\} = sup \left\{ \frac{1}{1} \right\} = 1)
Par conséquent on a que pour tout entier n,
Donc on a trouvé une suite non nulle
Mais je ne vois pas en quoi ça veut dire que |
------------------------------------------
Update:
Si je reprends la définition de
Re: Norme opérateur
Tu vois l'idée, mais encore une fois ce que tu écris dans la dernière ligne n'est pas correct.
Essaie de faire mieux. Je te laisse pour ce soir.
Essaie de faire mieux. Je te laisse pour ce soir.
Re: Norme opérateur
Etant donné que j'ai montré qu'on a trouvé une suite non nulle _n=1) tel que
tel que _n)
De plus_n||=1) et
et _n||=1) alors cela implique que
alors cela implique que 
On a montré précédemment que
PAr conséquent
De plus
On a montré précédemment que
PAr conséquent
Re: Norme opérateur
OK, tu as juste oublié "telle que _n)=(x_n)_n) ".
".
C'est une démarche assez fréquente pour déterminer la norme d'un opérateur : trouver une constante telle que
telle que \Vert \leq C\,\Vert x\Vert) pour tout
pour tout  , et exhiber un
, et exhiber un  tel que
tel que \Vert = C\,\Vert x\Vert) ; on en déduit
; on en déduit  .
.
C'est une démarche assez fréquente pour déterminer la norme d'un opérateur : trouver une constante
Re: Norme opérateur
D'accord, dans cet exercice alors 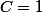
Mais ne peut-on pas du coup juste montrer qye||\leq ||x||) pour tout x, après on a aussi montré que
pour tout x, après on a aussi montré que || = ||x||) donc en déduit
donc en déduit  (sans dire que
(sans dire que  )
)
J'avais une autre question, pour la continuité de . Ici E est l'espace vectoriel des suites réelles bornées mais cela veut pas forcément dire que
. Ici E est l'espace vectoriel des suites réelles bornées mais cela veut pas forcément dire que  est de dimension finie donc je peux pas utiliser le théorème qui dit que si
est de dimension finie donc je peux pas utiliser le théorème qui dit que si  est finie alors tout
est finie alors tout ) est continue.
est continue.
Mais est-ce que je peux utiliser le fait que) est bornée donc
est bornée donc  est uniformément continue donc
est uniformément continue donc  est continue
est continue
Mais ne peut-on pas du coup juste montrer qye
J'avais une autre question, pour la continuité de
Mais est-ce que je peux utiliser le fait que
Re: Norme opérateur
CorentinD a écrit:après on a aussi montré que
Je dirais plutôt "on a aussi montré qu'il existe un
CorentinD a écrit:est bornée donc
est uniformément continue donc
est continue
Que veux-tu dire exactement par "
Re: Norme opérateur
Oui c'est vrai ! Ce que je voulais dire c'est que la méthode ce n'est pas qu'il faut montrer que et
et  donc
donc 
A est l'espace vectoriel des suites réelles bornées donc je pensais que A était lui-meêm borné
A est l'espace vectoriel des suites réelles bornées donc je pensais que A était lui-meêm borné
Re: Norme opérateur
"A est l'espace vectoriel des suites réelles bornées donc je pensais que A était lui-meêm borné"
Non, ça ne tient pas debout.
Mais je pense que tu sais ce qu'il faut faire pour montrer qu'une application linéaire entre espaces vectoriels normés est continue ? (Revois ton cours si besoin).
Non, ça ne tient pas debout.
Mais je pense que tu sais ce qu'il faut faire pour montrer qu'une application linéaire entre espaces vectoriels normés est continue ? (Revois ton cours si besoin).
Re: Norme opérateur
Il y aurait des choses à dire sur ce que tu as écrit, mais je commence à fatiguer.
Et puis, on a déjà vu que_n)\Vert \leq \Vert (x_n)_n\Vert) pour toute suite bornée
pour toute suite bornée _n) , ce qui assure la continuité de
, ce qui assure la continuité de  .
.
Et puis, on a déjà vu que
Re: Norme opérateur
Oui on peut le montrer comme cela aussi ,merci !
Je vous remercie sincéremment pour toutes vos réponses et votre patience
Je vous remercie sincéremment pour toutes vos réponses et votre patience
39 messages
- Page 2 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 48 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
