Voisinage
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
CorentinD
- Membre Naturel
- Messages: 57
- Enregistré le: 19 Mar 2020, 10:13
-
par CorentinD » 07 Oct 2020, 08:33
Bonjour à toutes et à tous !
J'ai un petit exercice qui me pose problème. Voici l'énoncé :
On pose:
 \rightarrow (1+x -y^2, 1+x^2+2y+y^3) <br />\end{cases})
Vous montrerez l'existence d'un voisinage
de
 \ R^2)
et d'un voisinage
de
\in R^2)
tel que
restreint à
:
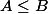
est inversible.
On notera
son inverse et vous déterminerez le polynôme de Taylor d'ordre 1 de
au point
)
Où j'en suis dans mon exercice ?Déjà pour montrer l'existence d'un voisinage
j'ai commencé par calculer :
=(1,1))
Mais après je ne vois plus quoi faire. A vrai dire je n'arrive pas à faire le lien et utiliser l définition de voisinage que je rappelle : un voisinage d'un point est une partie de l'espace qui contient un ouvert qui comprend ce point.
Bonne journée
-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
par GaBuZoMeu » 07 Oct 2020, 09:44
Bonjour,
N'aurais-tu pas vu le théorème d'inversion locale dans ton cours ?
-
CorentinD
- Membre Naturel
- Messages: 57
- Enregistré le: 19 Mar 2020, 10:13
-
par CorentinD » 07 Oct 2020, 14:00
Ooui j'ai vu le théorème d'invrsion locale, je le rappelle :
Soit E,F complets,
f :
une fonction de classe
et soit
tel que
 _in L(E,F))
soit bijctive (donc inversible). Alors il existe un voisinage
de
et voisinage
de
)
tel que :
f restreint à
est inversible
Donc je vais me servir de ce théorème pour répondre à la question .
Il faut d'abord que je montre que
est complet c'est à dire il faut que je montre que toute suite de cauchy converge. Ou utiliser la norme supérieure maos je ne sais pas comment m'y prendre avec cette fonction ...
Ensuite je montre que
est de classe
en dérivant
)
= \begin{pmatrix}<br />1 & -2y \\ <br /> 2x & 2+3y^2<br />\end{pmatrix})
Or
 \in R^2)
donc
 \in R^2)
-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
par GaBuZoMeu » 07 Oct 2020, 14:22
Bah, tu es en dimension finie ! Il n'y a pas de problème de complétude.
Que racontes tu avec
\in \R^2)
??? Tu vois bien que c'est une application linéaire de
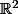
dans lui-même.
-
CorentinD
- Membre Naturel
- Messages: 57
- Enregistré le: 19 Mar 2020, 10:13
-
par CorentinD » 07 Oct 2020, 14:38
Oui
Ce que je voulais dire c'est que f est de classe
parce que sa dérivée appartient à
-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
par GaBuZoMeu » 07 Oct 2020, 14:54
Ce que tu voulais dire ne fait pas sens.
-
CorentinD
- Membre Naturel
- Messages: 57
- Enregistré le: 19 Mar 2020, 10:13
-
par CorentinD » 07 Oct 2020, 15:06
Oui je me doute, en fait je veux vérifier toutes les conditions pour appliquer le théroème.
Par conséquent, il faut que je montre que
est une fontion de classe
. C'est pour cela j'ai voulu faire
)
Si je reprends :
Soit
 : \left\lbrace\begin{matrix}<br />R^2 \rightarrow R^2\\ <br />(x,y) \rightarrow \begin{pmatrix}<br />1 & -2y\\ <br />2x & 2+3y^2<br />\end{pmatrix} <br />\end{matrix}\right.)
Or,
Donc
foncton de classe
On a
 \in R^2)
Montrons que
 \in L(R^2,R^2))
=\begin{pmatrix}<br /> 1 & 0 \\ <br />0 & 2<br />\end{pmatrix})
Donc
 \in L(R^2,R^2))
On doit montrer qur
est bijective
Notons
Calculons
,
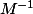
Donc M est inversible donc
est bijective
Alors d'après le théorème,
il existe un voisinage de
de
)
et voisinage
de
 = (1,1))
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 50 invités
