Bonjour,
Nous savons que si P est résoluble par radicaux, toute racine de son corps de décomposition sur Q s’exprime à l’aide des 4 opérations et des racines énièmes.
Réciproquement si toutes les racines de la clôture algébrique de Q dans C s’expriment à l’aide des 4 opérations et de racines énièmes, quelle est l'extension R du corps de décomposition de P telle que R soit une extension par radicaux de Q?
Merci d'essayer de m'éclairer sur ce point.
Extension radicale
6 messages
- Page 1 sur 1
Re: extension radicale
Bonjour
Désolé, mais je ne comprends absolument pas cette question. Les nombres algébriques ne s'expriment certainement pas tous "à l’aide des 4 opérations et de racines énièmes".
Et le corps de décomposition d'un polynôme ne s'étend pas en général en une extension résoluble de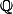 .
.
Peux-tu reformuler ta question plus clairement ?
Réciproquement si toutes les racines de la clôture algébrique de Q dans C s’expriment à l’aide des 4 opérations et de racines énièmes, quelle est l'extension R du corps de décomposition de P telle que R soit une extension par radicaux de Q?
Désolé, mais je ne comprends absolument pas cette question. Les nombres algébriques ne s'expriment certainement pas tous "à l’aide des 4 opérations et de racines énièmes".
Et le corps de décomposition d'un polynôme ne s'étend pas en général en une extension résoluble de
Peux-tu reformuler ta question plus clairement ?
Re: extension radicale
Je sais bien que tous les nombres ne s'expriment pas à l'aide des 4 opérations et des racines énièmes.
Je sais en revanche que si P est u polynôme résoluble par radicaux alors toutes les racines de son corps de décomposition s'expriment à l'aide des 4 opérations et des racines énièmes.
La question que je me pose est la réciproque de la propriété précédente:
Si toutes les racines de son corps de décomposition s’expriment à l'aide des 4 opérations et des racines énièmes, quelle est l'extension radicale de son corps de décomposition autrement dit si je sais qu'il y a une extension radicale cela voudra dire qu'il est résoluble par radicaux
Je ne sais pas formuler plus clairement ma question.
Merci
Je sais en revanche que si P est u polynôme résoluble par radicaux alors toutes les racines de son corps de décomposition s'expriment à l'aide des 4 opérations et des racines énièmes.
La question que je me pose est la réciproque de la propriété précédente:
Si toutes les racines de son corps de décomposition s’expriment à l'aide des 4 opérations et des racines énièmes, quelle est l'extension radicale de son corps de décomposition autrement dit si je sais qu'il y a une extension radicale cela voudra dire qu'il est résoluble par radicaux
Je ne sais pas formuler plus clairement ma question.
Merci
Re: extension radicale
Si l'équation est résoluble par radicaux, le corps de décomposition lui-même n'est-il pas une extension résoluble du corps de base ???
Franchement, je ne comprends toujours pas ta question.
Franchement, je ne comprends toujours pas ta question.
Re: extension radicale
Bonjour,
En fait, lorsque les racines du corps de décomposition du polynôme s’écrivent à l'aise des 4 opérations et des racines énièmes je cherche juste à exhiber une suite des corps qui définissent l'extension radicale du corps de décomposition sur Q du polynôme. C'est cette suite de corps que je n'arrive pas à trouver.
Or tu prends le problème à l'envers : je sais en effet que si l'équation est résoluble par radicaux, il existe une extension radicale du corps de décomposition, mais ce n'est pas cela que je demande, c'est la réciproque.
En fait, lorsque les racines du corps de décomposition du polynôme s’écrivent à l'aise des 4 opérations et des racines énièmes je cherche juste à exhiber une suite des corps qui définissent l'extension radicale du corps de décomposition sur Q du polynôme. C'est cette suite de corps que je n'arrive pas à trouver.
Or tu prends le problème à l'envers : je sais en effet que si l'équation est résoluble par radicaux, il existe une extension radicale du corps de décomposition, mais ce n'est pas cela que je demande, c'est la réciproque.
Re: extension radicale
Tu es toujours aussi confus dans ton expression, et si je "prends le problème à l'envers", c'est parce que tu as toi-même de grosses difficultés à l'exposer dans le bon sens.
Dois-je comprendre, à la lecture du premier paragraphe du message précédent, que tu cherches à écrire une extension galoisienne résoluble de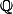 comme une suite d'extension cycliques ?
comme une suite d'extension cycliques ?
Dois-je comprendre, à la lecture du premier paragraphe du message précédent, que tu cherches à écrire une extension galoisienne résoluble de
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 29 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
