Temps de déplacement d'un moteur de volet roulant

[Ben314]

Salut,
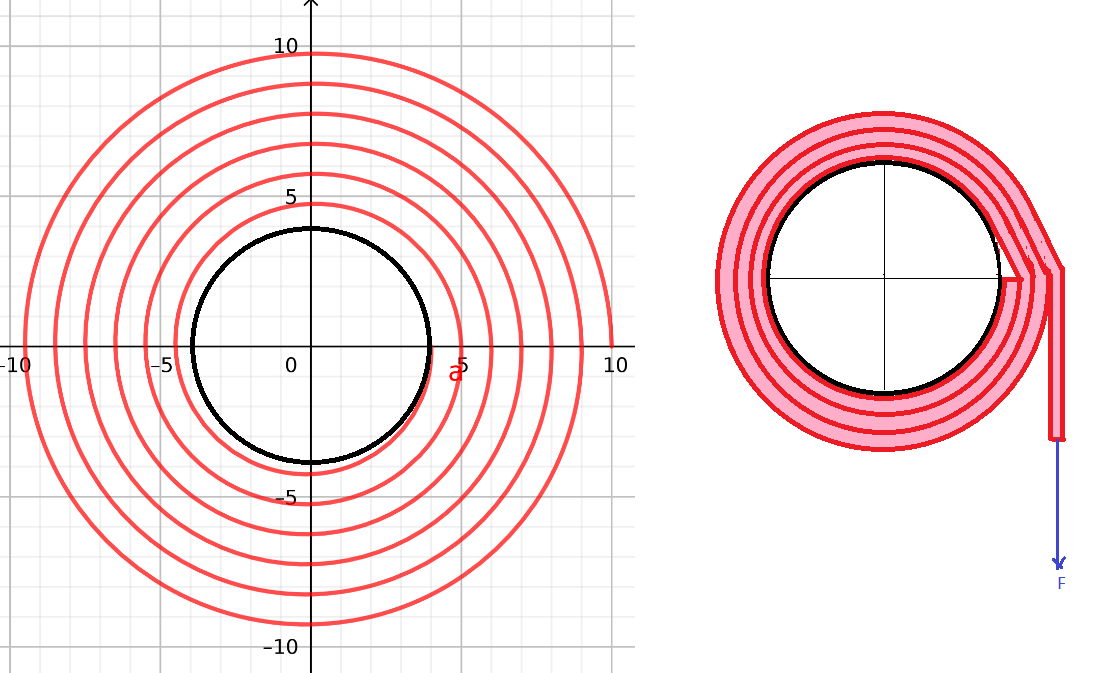
GaBuZoMeu te l'a dit : si tu veut une formule "simple" qui approxime ton truc, tu considère que l'enroulement se fait en suivant une spirale logarithmique. Tu va avoir une petite erreur lié au fait que, sur les premiers tours, l'enroulement va plutôt avoir un "saut" à un endroit précis, mais à mon avis ça sera plus que largement suffisant comme approximation.
Dans ce cas, la courbe donnant l'enroulement du volet va âtre de la forme avec (en seconde) et où sont des constantes à déterminer :
- La constante , c'est le rayon de l'axe sur lequel s'enroule le rideau donc à priori, ça devrait être le 3cm dont tu parle dans ton premier post.
- La constante correspond à la vitesse de rotation (en radian par seconde) et vu tes données ça devrait être .
- La constante , elle est liée à l'espacement entre deux spire (qui vaut cm) et tu peut l'obtenir soit en mesurant directement cet espacement, soit, plus bêtement, en mesurant la longueur du volet (ou plus précisément la longueur de la partie qui s'enroule).

Ensuite, une fois ces constantes déterminées, la longueur qui sera enroulé en un temps , ça sera qui se calcule relativement bien.

[Black Jack]

On peut avoir un tel type de dépendance avec la modélisation par la spirale d'Archimède qui ne me semble pas mauvaise, malgré ce qu'en dit BlackJack. Disons, pas plus mauvaise que celle qu'il utilise.

Aucun besoin de la spirale d'Archimède ... qui ne représente pas mieux la réalité que le modèle que j'ai utilisé.
... qui est aussi peu précis, plus le rayon du rouleau est petit devant la taille des lames (donc encore pire maintenant que les données ont été changées, voir les *** en fin de message)
Cela reste néanmoins plus que bon assez vu toutes les imprécisions qui accompagnent sans aucun doute l'énoncé.

14,3 s à 17 tr/min --> 4 tours moteur

L = 2Pi * (2 + 3,5 + 5 + 6,5) = 107 cm

107 cm de volet étendu --> 107 * 3,7/(3,7 + 0,5) = 94 cm de lames jointives.

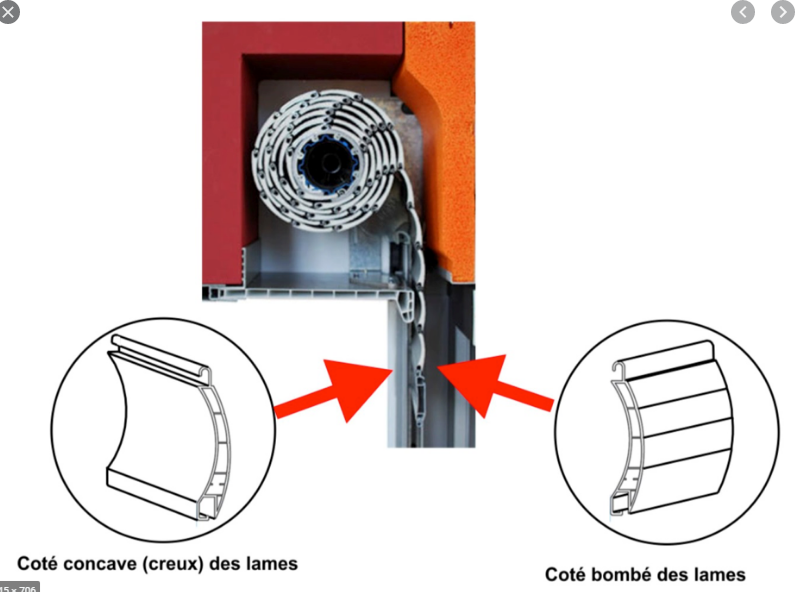
Sur les 1er (107 - 94) = 13 premiers cm de "tirage" vers le haut, les lames vont "s'écarter" mais la lame du bas restera au sol.

Le 1er tour moteur correspond à 2*Pi*2 = 12,6 cm (presque 13 cm)

--> pendant 1/17 s, les lames vont s'écarter mais avec la lame du bas restant au sol.

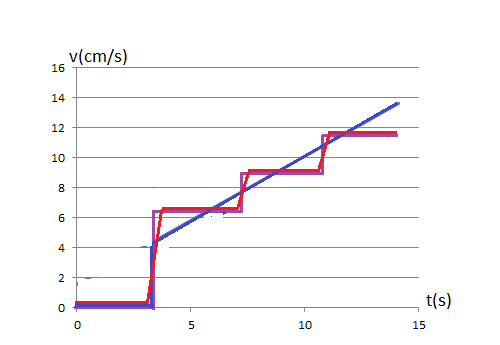
Pendant le 2eme tour moteur, le volet montera de 2Pi * (2+1,5) = 22 cm en 1/17 min (soit 3,53 s)--> (donc à v = 6,2 cm/s)

Pendant le 3eme tour moteur, le volet montera de 2Pi * (2+1,5+1,5) = 31,4 cm en 1/17 min (soit 3,53 s) (donc à v = 8,9 cm/s)

Pendant le 4eme tour moteur, le volet montera de 2Pi * (2+1,5+1,5+1,5) = 40,8 cm en 1/17 min (soit 3,53 s) (donc à v = 11,5 cm/s)
****
Présenté autrement :

- Le volet écarte ses lames sans bouger celle du bas pendant 3,53 s
- La lame du bas monte de 22 cm (donc se retrouve à 22 cm du sol) en 3,53 s, à la vitesse de 6,2 cm/s
- La lame du bas monte de 31,4 cm (donc se retrouve à 53,4 cm du sol) en 3,53 s, à la vitesse de 8,9 cm/s
- La lame du bas monte de 40,8 cm (donc se retrouve à 94,2 cm du sol) en 3,53 s, à la vitesse de 11,5 cm/s

*** Ceci à quelques pour cent près ... car il n'est pas tenu compte que les lames rigides ne s'enroulent pas en cercles parfaits.

[Olivierdar]

Est ce que c'est totalement faux de dire que la vitesse peut s'exprimer en V(t) = 0.7648 * t + 6.2
après les 13 premiers cm.

[Black Jack]

"Disons, pas plus mauvaise que celle qu'il utilise."

Pas meilleure non plus.

Ceci (hors déformations dues à la rigidité des lames) :



... ressemble plus à des cercles presque complets qui sautent sur le précédent sur quelques cm qu'à une spirale d'Archimède pour laquelle une "spire" s'éloigne partout de plus en plus de la précédente.

Cela ne signifie pas qu'une méthode avec spirale d'Archimède conduira à une mauvaise approximation ... mais pas meilleure que celle que j'ai utilisée (qui est aussi évidemment une approximation)

[Black Jack]

Dessin plus joli ... et tout aussi explicite.
Un tour s'appuie sur le précédent sur la presque totalité du tour et "saute" à la couche suivante sur une très courte distance.

[GaBuZoMeu]

Où vois-tu un saut ? Cette photo colle assez avec le modèle de la spirale d'Archimède, je trouve.

[Black Jack]

On ne voit pas l'épaisseur de ton volet, ni le tambour
Si tu les représentais, tu verrais ce qui ve va pas.

La première "spire" DOIT "coller" au tambour sur la quasi totalité du tour. (sous l'effet du poids du volet qui est en grande partie vertical lorsque la 1ere spire s'enroule)
Il n'y a aucune raison que la spire s'écarte du tambour sans l'intervention d'un coup de baguette magique.

La 1ere spire, qui DOIT coller au tambour ne s'en écarte qu'à la toute fin du tour pour "grimper" sur l'épaisseur du volet au niveau du début du 2eme tour.

Le 2ème tour DOIT "coller" sur le 1er tour sur la quasi totalité du tour.
Il n'y a aucune raison que la 2eme spire s'écarte de la première sans l'intervention d'un coup de baguette magique.

La 2éme spire, qui DOIT coller à la première ne s'en écarte qu'à la toute fin du tour pour "grimper" sur l'épaisseur du volet au niveau du début du 3eme tour.

...
*********
Le dessin de gauche est physiquement impossible. (en noir, j'ai ajouté le tambour)
Le poids du volet oblige chaque tour à coller au précédent et cela impose des "sauts" en fin de chaque tour pour grimper sur l'épaisseur.

On est donc dans le cas dessiné à droite.

[GaBuZoMeu]

Oui, c'est absolument frappant sur la photo que tu as toi-même fournie que ton "saut à chaque tour" est une meilleure modélisation de la réalité que la spirale d'Archimède !



la rigidité des lattes montre que l'histoire du "saut" n'est pas très crédible.

[Black Jack]

Oui, c'est absolument frappant sur la photo que tu as toi-même fournie que ton "saut à chaque tour" est une meilleure modélisation de la réalité que la spirale d'Archimède !



la rigidité des lattes montre que l'histoire du "saut" n'est pas très crédible.

Libre à toi, de vouloir modifier les lois de la physique pour qu'elles se plient à ta spirale ...
Mais la physique ne se plie pas à ces caprices.

Si tu continues à ne pas voir que le 1er tour colle au mandrin (soit qu'il touche le mandrin sur chacune de ses petites articulations inter lame (et même ici en plus près du milieu de chaque lame) et que cela ne s'écarte de l'épaisseur du volet après chaque tour complet, alors c'est pour le moins inquiétant.

je serais très intéressé que tu me précises la loi physique qui ferait que "l'enroulement" du 1er tour s'écarte du mandrin sur toute sa longueur.

Dans le message du 29 Mai 2020 17:33, sur le dessin de gauche ... où j'ai ajouté le mandrin, je serais très intéressé que tu me précises la loi physique qui ferait que "l'enroulement" du 1er tour s'écarte du mandrin sur toute sa longueur.

Inutile de tenter de noyer le poisson via la rigidité des lattes (d'ailleurs pas si rigide que cela), c'est un problème qui n'a rien à voir avec le fait que la spirale n'est pas un modèle physiquement possible, c'est une grosse approximation, qu'on peut utiliser si on veut ... mais moins proche de ce qui se passe que le modèle plus simple que j'ai employé.

Le 1er tour "colle" au mandrin en le touchant à chaque articulation de lame mais aussi (grâce à la flexion des lames, non infiniment rigides) près du milieu de chaque lame.

Donc on peut dire que le 1er tour qui est en contact avec le mandrin en un bon nombre de points répartis sur la presque totalité du tour, est "collée" au mandrin.

... Jusqu'à ce qu'il doive s'en écarter (d'une épaisseur de lame) pour monter sur le début de la 1ere spire . Cela se voit parfaitement sur le dessin.

Pour les tours suivant, on voit très bien qu'un tour s'appuie sur le précédent par chacune des articulations interlames. c'est ce que j'appelle une spire "colle" à la précédente jusqu'au moment de sauter au dessus du début du tour ... et que donc le "rayon" du tour est constant sur presque la totalité du tour (jusqu'au saut) en fin de tour (et non le "rayon" n'augmente pas sur la totalité du tour comme dans une spirale).

Essayer de cacher le problème en ne dessinant pas le mandrin, ni l'épaisseur du volet ne change en rien le problème.

J'en reste là.

[Ben314]

Perso (et histoire de rajouter un peu d'huile sur le feu...), en regardant la photo, ça me donne très nettement l'impression que le tambour d'enroulement n'est pas rond, mais dessine le début d'une spirale (de façon à ce que, justement, il n'y ait pas de saut au début du 2em enroulement).

[GaBuZoMeu]

Bof ! (Ça s'adresse à BlackJack, pas à Ben).

Une petite question : qui, dans sa première réponse, est complètement passé à côté du problème de l'augmentation du rayon du cylindre au cours de l'enroulement ? Qui a tout de suite signalé ce problème ?
J'ai proposé le modèle de la spirale. C'est bien sûr une approximation, mais une approximation qui n'est pas déraisonnable. L'équation de la spirale est . L'élément de longueur sur la spirale est , dont l'intégration de 0 à est

[Black Jack]

Bonjour Ben,

Ben ...

Non le mandrin n'est pas un début de spirale, ceci est impossible, sinon il y aurait un décalage de niveau entre le début du mandrin et sa fin (qui sont évidemment au même niveau)

Le mandrin n'est en général pas cylindrique, le plus souvent, il est octogonal ou plus rarement, il présente de petites dents sur la périphérique de son âme cylindrique.

Ceci pour permettre un bon accrochage (en diminuant les risques d'arrachement des attaches par glissement du volet du le mandrin) et parfois (rarement), ils sont parfaitement cylindriques.

En voila 2 représentations (tirées de la doc sur les volets mécaniques et pas issues de mon imagination)



Par la pesanteur (poids du volet non encore enroulé), une "spire" est obligée de "coller" à la précedente, elle ne peut en aucun cas s'en écarter, ce qui rend le modèle de la spirale impossible.

Ceci ne signifie pas que le modèle de la spirale ne peut pas être utilisé, mais à choisir entre 2 modèles imparfaits, si un des deux est plus simple (même rien qu'un peu) à utiliser et plus proche de la réalité, il n'y a pas à hésiter.

En pratique, on aura bien (à vitesse de moteur de mandrin constante), la vitesse de montée du volet qui varie par paliers et pas de manière continue.

Mon modèle simplifié, passe d'un niveau de vitesse au suivant par "escalier", alors qu'en pratique, il va passer d'un palier à l'autre par une "rampe" ... qui sera courte en temps (lorsqu'un tour "monte" sur le précédent), environ la durée de passage d'une lame au niveau du saut.

L'autre modèle, la spirale, va donner une vitesse qui grimpe sans à coup ... peut-être plus harmonieux, mais surtout moins représentatif de la réalité.

[Black Jack]

Bof ! (Ça s'adresse à BlackJack, pas à Ben).

Une petite question : qui, dans sa première réponse, est complètement passé à côté du problème de l'augmentation du rayon du cylindre au cours de l'enroulement ? Qui a tout de suite signalé ce problème ?
J'ai proposé le modèle de la spirale. C'est bien sûr une approximation, mais une approximation qui n'est pas déraisonnable. L'équation de la spirale est . L'élément de longueur sur la spirale est , dont l'intégration de 0 à est

Certes, ma première réponse était à l'image des données fournies par le problème.
Ces données étaient tout à fait "hors réalité" et il n'était pas utile (à tort ?) alors de pousser le raisonnement.

Certains ont demandé des données supplémentaires (alors que c'était inutile) et sans s'apercevoir que les données fournies conduisaient à des inepties.
Cela s'est vérifié, quand les données ont été corrigées ... ce qui a conduit à un volet plus court d'un facteur 5 et confirmé que la donnée supplementaire demandée avant était inutile car redondante avec celles fournies.
La longueur a été calculée dans un de mes messages à partir des données fournies et ... miracle a collé avec la donnée de la longueur fournie (qui était donc bien redondante).

Le tout n'est pas d'avoir une "formule" de longueur enroulée qui se calcule bien mais surtout une qui est le plus possible représentative.

Un modèle doit se rapprocher le plus possible des lois physiques qui régissent le problème et pas l'inverse.

En pratique, on aura bien (à vitesse de moteur de mandrin constante), la vitesse de montée du volet qui varie par paliers et pas de manière continue.

Mon modèle simplifié, passe d'un niveau de vitesse au suivant par "escalier", alors qu'en pratique, il va passer d'un palier à l'autre par une "rampe" ... qui sera courte en temps (lorsqu'un tour "monte" sur le précédent), environ la durée de passage d'une lame au niveau du saut.

L'autre modèle, la spirale, va donner une vitesse qui grimpe sans à coup ... peut-être plus harmonieux, mais surtout moins représentatif de la réalité.

Maintenant, Olivierdar fera ce qu'il veut, il choisira la méthode qu'il veut.

Si, comme c'est probable, il a les pieds sur Terre, il aura vite compris ce qu'il doit faire.

[Black Jack]

Pour en terminer vraiment (pour moi)

En tenant compte que le 1er tour moteur ne fait qu'écarter les lattes, voila ce que cela donne pour la vitesse de montée de la latte du bas.

Courbe en rouge : représentation de la vitesse réelle.
Courbe en mauve : représentation par mon modèle
Courbe en bleu : représentation par le modèle de la spirale.

Comme la question est posée sur la vitesse en fonction de la position, le choix entre les modèles est évident.



En pratique, il y a de petits "cahots" dans la vitesse vu la forme des lattes qui n'a pas été prise en compte dans aucun des 2 modèles, ceci ne change rien de fondamental pour le choix du modèle.

[GaBuZoMeu]

Je viens juste de baisser à mi-hauteur le volet roulant juste devant mon bureau pour me protéger du soleil. Et la

Courbe en rouge : représentation de la vitesse réelle.

de Black Jack me fait rigoler.
C'est une courbe résultant d'une mesure sur un volet roulant en fonctionnement ?

[Black Jack]

Rigole tant que tu veux.

Mais abstiens-toi dorénavant de répondre à un problème où un zeste de loi physique entre en jeu.
C'est ridicule et tu pousses le novice à partager ton incompétence.

[Black Jack]

Mesure sur un de mes volets

Je monte le volet jusqu'à ce que tous les interstices inter-lame soient ouverts.

Le mandrin sur lequel s'enroule le volet fait environ 8 cm de diamètre (octogone) (partiellement enroulé à cause de la montée pour ouvrir les interstices inter-lame), la courroie de commande (manuelle) s'enroule sur un tambour d'environ 15 cm de diamètre et la courroie a une épaisseur d'environ 1,5 mm.

Je marque la courroie par des traits espacés de 12 cm.

Je tire sur la courroie pour la faire bouger 12 cm à chaque fois. (je le fais 9 fois, suffisant pour comprendre)

Je mesure de combien monte le volet à chaque fois ... les mesures sont :

6,8 cm ; 6,8 cm ; 6,8 cm ; 6,8 cm ; 7,0 cm , 7,5 cm ; 8,3 cm ; 8,3 cm ; 8,3 cm (mesures à environ 1 ou 2 mm près)

Conclusion :

Le volet reste à montée constante sur tout un tour.
La montée augmente lors du saut sur le tour suivant.
Le tour se poursuit à montée constante sur tout le tour (mais avec une montée plus forte que sur le tour précédent)

No comment.

[GaBuZoMeu]

@BlackJack.
J'ai toujours écrit que le modèle de la spirale est une approximation. Sans doute moins bonne quand le volet est presque déroulé et qu'on est près de l'axe, et sans doute meilleure quand le volet est presque enroulé et qu'on est plus loin de l'axe. Quand je fais marcher le volet de ma porte fenêtre de la position "tout enroulé" à la position "mi-hauteur", aucune variation brusque de vitesse marquant des "sauts". La qualité de l'approximation dépend aussi sans doute des modèles de volet roulant, de la forme de l'axe et de la façon dont la première latte est attachée à l'axe. Visiblement dans la première photo que tu as fournie ce n'est pas au moyen d'une sangle sur un axe octogonal, et tu as d'ailleurs été bien incapable de localiser sur cette photo les "sauts" que tu fais figurer sur ton schéma. Bref, tu t'énerves et tu m'insultes pour pas grand chose.

@Olivierdar : j'ai donné plus haut l'élément de longueur pour une spirale, qui donne une vitesse

Le petit 1 sous la racine carrée peut sans doute être négligé sans grand dommage, ce qui aboutit à

conforme à ce que tu as écrit plus haut.
La formule pour la longueur enroulée se simplifie alors en

Je pense que tu peux valablement travailler avec ça. Tu nous dira si ça te convient.

[Black Jack]

"Quand je fais marcher le volet de ma porte fenêtre de la position "tout enroulé" à la position "mi-hauteur", aucune variation brusque de vitesse marquant des "sauts". "

Tout simplement parce que ce n'est pas évident de s'en rendre compte, mais ils sont bien là.
L'amplitude des sauts dépend évidemment du "diamètre" du mandrin et de "l'épaisseur" des lames et peut donc être plus ou moins visibles en fonction du volet.

Et bien entendu que plus on a enroulé de tours, moins grand sont les "sauts" de vitesse et plus on se rapproche de la vitesse calculée via la spirale ... ce qui n'empêche pas que la vitesse calculée via le modèle spirale est toujours plus éloigné de la réalité que la vitesse calculée via le modèle à "sauts" .

Si on veut faire des mesures pratiques, on peut faire ce que j'ai fait ... mais ce n'est possible que sur un volet à "commande" manuelle par une courroie par exemple.
Pour un volet électrique, la seule manière convenable serait de filmer la montée à une cadence d'images connue (avec un repère sur le volet et une "toise" immobile qui permet de mesurer le déplacement ... et d'en déduire la vitesse en fonction de la position par analyse de la séquence d'images.

Dans le cas pratique du volet décrit, l'enroulement ne se fait que sur 4 tours et on a bien (même si cela te fait rigoler à tort) quelque chose de très proche des dessins du message du 30 Mai 2020 14:08.

Si le but est d'utiliser un logiciel simpliste et qu'on se contente d'une mauvaise précision surtout sur les 1er tours d'enroulement (mais ici il n'y en a que 4) ... on peut utiliser le modèle spirale.
Si on veut plus coller à la réalité (je ne connais pas le vrai but de l'auteur de la question), alors, le modèle à sauts s'impose ... sachant que ce n'est aussi qu'une approximation, mais plus proche de la réalité.

[Black Jack]

"tu as d'ailleurs été bien incapable de localiser sur cette photo les "sauts" que tu fais figurer sur ton schéma."

Faux, ils sont tellement visibles qu'il faut être aveugle pour ne pas les voir.
Comme cela semble être ton cas, je donne les infos suivantes (avec peu d'espoir d'être compris)



Je repère par un point rouge les lattes du 1er tour.
Après un tour complet (à rayon constant), la latte repérée en bleu effectue le saut
Les lattes du tour suivant (à plus grand rayon constant) sont repérées en vert
Après un tour complet, le saut est effectué par la latte repérée en mauve.
Les lattes du tour suivant (à plus grand rayon constant) sont repérées en rose
...

Chaque tour colle au précédent.
Evidemment, à cause de la forme des lattes (et notamment les articulations inter lattes), il semble y avoir des interstice entre les tours ...
ce n'est pas du à un effet quelconque de spirale, chaque latte est en contact à celle(s) du tour précédent et donc le "rayon" d'un tour est constant.

Et bien entendu, le volet de cette photo, n'est pas celui de l'auteur de la question, ni celui sur lequel j'ai fait les mesures chez moi.
C'est évident. Cela ne change rien de rien à la problématique.