Determiner la loi de variables aléatoires avec une loi unifo

[Elodie37]

Bonjour ,
Voici l'énoncé de mon exercice :
Soit X une variable aléatoire strictement positive et lambda un réel strictement positif. On définit les variables aléatoires U et V par : U=1-X et
V=-(ln(x)/lambda). Déterminer les lois de U et V si X suit une loi uniforme sur [0,1].
J'ai donc commencer par définir la loi de densité de X qui est 1 car f(x)=1/(b-a)=1/1=1
Mais après je ne sais pas du tout quoi faire , j'ai chercher dans tous les exercices que nous avons fait en cours et sur internet mais je ne trouve rien de similaire
Si quelqu'un peut m'aider je le/la remercie d'avance

[GaBuZoMeu]

Bonjour,

Si tu as des problèmes à manipuler la densité, tu peux passer par la fonction de répartition.

équivaut à quel événement concernant ?
Même question pour .

[Elodie37]

Merci de mavoir répondu , ce n'est pas le calcul avec la loi de densité qui me pose probleme , c'est le fais quon ne peut calculer qu'un intervalle avec la loi de densité et je ne comprend pas quel intervalle je dois calculer pour avoir la loi de U et V. De plus , pour V je ne vois pas comment utiliser la loi de densité car il y a un lambda dans son calcul.
Ps : Désolé de ne pas avoir préciser mes problème spécifique

[GaBuZoMeu]

Tu es allé poser ta question sur un autre forum sans tenir compte de la piste que je t'ai indiquée et en réponse tu as eu ... la même piste !

Je répète : passe par les fonctions de répartition. Pour calculer la probabilité de , compte tenu du fait que 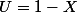, tu dois réaliser ce que veut dire l'événement pour .
Ce n'est tout de même pas la mer à boire, si tu veux bien y réfléchir !

[tournesol]

Je note F les fonctions de répartitions .
Montre moi que
Après je t'aiderai ( pas avant 23 h)

[Elodie37]

Fu(X)=P(U<=t)=P(1-X<=t)=P(X>=1-t)=1-P(X<1-t)=
1-Fx(-(1-t))=1-Fx(1-t)
Merci pour ta réponse

[GaBuZoMeu]

Tu pourrais aller un peu plus loin ?
Je pense que tu connais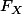 , la fonction de répartition pour la loi uniforme sur .

[tournesol]

Ce n'est pas mais .
Sinon ta démo est correcte .
Il ne te reste plus qu'à dériver , puis à déterminer sur quel intervalle 1-t appartient à [0;1] .
Enfin tu peux appliquer la même méthode pour V .

[Elodie37]

merci tournesol vous m'avez bien aider , j'ai réussi a finir mon exercice.

[tournesol]

As tu trouvé que V suit une loi exponentielle ?