Bonjour !
Dans un exercice, on me donne la fonction f suivante :
f(x) = e^{x} + ax + be^{-x}
On me demande ensuite de calculer f'(x) pour tout réel x, et là je beug un peu, alors un peu d'aide ou une explication ne serait pas de refus ! Merci !
Fonction exponentielle
13 messages
- Page 1 sur 1
Re: Fonction exponentielle / Dérivée
J'ai conclus que la dérivée de e^{x} est e^{x}, que la dérivée de e^{-x} est - e^{-x} et que la dérivée de ax + b est a, ce qui donne :
f(x) ' = e^{x} + a * - e^{-x}
Et au final je trouve : f(x) ' = e^{x} + a (x + b)
Je suis pas très sûre mais..
f(x) ' = e^{x} + a * - e^{-x}
Et au final je trouve : f(x) ' = e^{x} + a (x + b)
Je suis pas très sûre mais..
jaderchb a écrit:Bonjour !
Dans un exercice, on me donne la fonction f suivante :
f(x) = e^{x} + ax + be^{-x}
On me demande ensuite de calculer f'(x) pour tout réel x, et là je beug un peu, alors un peu d'aide ou une explication ne serait pas de refus ! Merci !
Re: Fonction exponentielle / Dérivée
J'ai conclus que la dérivée de e^{x} est e^{x}, que la dérivée de e^{-x} est - e^{-x} et que la dérivée de ax + b est a, ce qui donne :
f(x) ' = e^{x} + a * - e^{-x}
Et au final je trouve : f(x) ' = e^{x} + a (x + b)
Je suis pas très sûre mais..
f(x) ' = e^{x} + a * - e^{-x}
Et au final je trouve : f(x) ' = e^{x} + a (x + b)
Je suis pas très sûre mais..
Mimosa a écrit:Bonjour
La dérivée d'une somme est la somme des dérivées.
Re: Fonction exponentielle / Dérivée
Les dérivées des exponentielles sont justes. Mais dans la somme tu rencontres ax, dont la dérivée est bien a. La somme des dérivées est donc 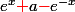
Re: Fonction exponentielle / Dérivée
Bonjour,
je crois qu'il manque le b de -be^(-x)
Donc,
f(x) = e^{x} + ax + be^{-x}
f'(x)=e^(x)+a-be^(-x)
Sauf si ta fonction était : f(x) = e^{x} + (ax + b)e^{-x} ce qui ne donnerait pas du tout la même chose
je crois qu'il manque le b de -be^(-x)
Donc,
f(x) = e^{x} + ax + be^{-x}
f'(x)=e^(x)+a-be^(-x)
Sauf si ta fonction était : f(x) = e^{x} + (ax + b)e^{-x} ce qui ne donnerait pas du tout la même chose
 Fonction exponentielle
Fonction exponentielle
Bonjour,
Je suis bloquée à la dernière question de mon DM de maths ! Voici l'énoncé :
On considère la fonction f définie pour tout réel x par f(x) = e^{x} + ax + be^{-x}, où a et b sont deux réels.
1) Lire graphiquement la valeur de f(0) et f'(0).
J'ai trouvé f(0) = 3 et f'(0) = -2
2) Calculer f'(x) pour tout réel x.
Grâce a l'aide de certaine personne ici, la réponse est f'(x)=e^(x)+a-be^(-x).
3) Déterminer les valeurs de a et b.
Ici, je ne sais pas si je dois utiliser la dérivée ou bien la fonction de base, si quelqu'un pouvait m'indiquer la méthode à suivre, merci !
Je suis bloquée à la dernière question de mon DM de maths ! Voici l'énoncé :
On considère la fonction f définie pour tout réel x par f(x) = e^{x} + ax + be^{-x}, où a et b sont deux réels.
1) Lire graphiquement la valeur de f(0) et f'(0).
J'ai trouvé f(0) = 3 et f'(0) = -2
2) Calculer f'(x) pour tout réel x.
Grâce a l'aide de certaine personne ici, la réponse est f'(x)=e^(x)+a-be^(-x).
3) Déterminer les valeurs de a et b.
Ici, je ne sais pas si je dois utiliser la dérivée ou bien la fonction de base, si quelqu'un pouvait m'indiquer la méthode à suivre, merci !
Re: Fonction exponentielle
Bonjour,
tu dois utiliser les 2 et tenir compte de f(0)=3, f'(0)=-2
tu obtiendras un système de 2 équations à 2 inconnues, à résoudre
tu dois utiliser les 2 et tenir compte de f(0)=3, f'(0)=-2
tu obtiendras un système de 2 équations à 2 inconnues, à résoudre
Re: Fonction exponentielle
D'accord, merci beaucoup !
Pisigma a écrit:Bonjour,
tu dois utiliser les 2 et tenir compte de f(0)=3, f'(0)=-2
tu obtiendras un système de 2 équations à 2 inconnues, à résoudre
Re: Fonction exponentielle
bonjour,
il est toujours dommage d'ouvrir plusieurs posts pour un même sujet ( lycee/fonction-exponentielle-derivee-t218185.html) car on ne peut pas suivre l'historique de ce qu'il s'est passé.
Ici, tu fais référence à l'aide que tu as déjà reçue, mais elle n'est plus visible et l'on ne sait pas quel chemin tu as alors suivi, et compris, pour arriver jusqu'à tes derniers écrits.
il est toujours dommage d'ouvrir plusieurs posts pour un même sujet ( lycee/fonction-exponentielle-derivee-t218185.html) car on ne peut pas suivre l'historique de ce qu'il s'est passé.
Ici, tu fais référence à l'aide que tu as déjà reçue, mais elle n'est plus visible et l'on ne sait pas quel chemin tu as alors suivi, et compris, pour arriver jusqu'à tes derniers écrits.
13 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 100 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
