Bonjour,
Il y a une finesse que je ne comprends pas :
Prenons f, un polynôme de degré 2 de la forme f(x) = ax^2+bx+c avec a>0,
Si on cherche le graphique de la fonction sachant que f(x)>=0,
Cela signifie que f(x) > 0 OU que f(x)=0, il suffit donc qu'au moins une des deux assertions soit vrai pour qu'on ait f(x)>=0 vrai.
On peut distinguer 2 cas,
(1) Pour que f(x)>0 soit vrai, il suffit que le minimum de la parabole soit strictement au dessus de l'axe des abscisses (car a>0).
(2) Pour que f(x) = 0 soit vrai, il suffit que la parabole "touche" l'axe des abscisses.
(3) La parabole touche en 1 point l'axe des abscisses.
Mais si la parabole touche l'axe des abscisses en, disons 2 points distincts, alors f(x)<0 entre ces deux points, ce qui contredit (1), ma question est donc, est-ce que cela est juste? Pour moi c'est faux car f(x)=0 sous entend pour tout x... Merci pour votre confirmation.
Bonne journée.
Question
5 messages
- Page 1 sur 1
Re: Question
Ta difficulté vient du fait que tu caches les quantificateurs sous le tapis
Tu étudies la situation où :
Pour tout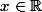
\geq 0)
Cela équivaut effectivement à :
Pour tout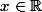 (
(> 0) ou
ou  = 0) )
)
Mais ça n'équivaut absolument pas à
( Pour tout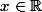 (
(> 0) ) ou (pour tout
) ou (pour tout 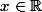
 = 0) )
)
10 secondes de réflexion devraient t'en persuader. C'est la même chose que "toutes les billes sont rouges ou bleues" qui n'est absolument pas équivalent à "toutes les billes sont rouges ou toutes les billes sont bleues".
Tu étudies la situation où :
Pour tout
Cela équivaut effectivement à :
Pour tout
Mais ça n'équivaut absolument pas à
( Pour tout
10 secondes de réflexion devraient t'en persuader. C'est la même chose que "toutes les billes sont rouges ou bleues" qui n'est absolument pas équivalent à "toutes les billes sont rouges ou toutes les billes sont bleues".
Re: Question
Bonjour,
"Si on cherche le graphique de la fonction sachant que f(x)>=0" n'a aucun sens mathématique tant que tu ne précises pas le quantificateur sur x ("il existe" ou "pour tout").
Par ailleurs, je n'ai pas vu de question posée dans ce que tu as écrit
"Si on cherche le graphique de la fonction sachant que f(x)>=0" n'a aucun sens mathématique tant que tu ne précises pas le quantificateur sur x ("il existe" ou "pour tout").
Par ailleurs, je n'ai pas vu de question posée dans ce que tu as écrit
Re: Question
GaBuZoMeu a écrit:C'est la même chose que "toutes les billes sont rouges ou bleues" qui n'est absolument pas équivalent à "toutes les billes sont rouges ou toutes les billes sont bleues".
Merci pour l'analogie!
Re: Question
LB2 a écrit:Bonjour,
"Si on cherche le graphique de la fonction sachant que f(x)>=0" n'a aucun sens mathématique tant que tu ne précises pas le quantificateur sur x ("il existe" ou "pour tout").
C'est noté.
Par ailleurs, je n'ai pas vu de question posée dans ce que tu as écrit
Moi non plus mais j'ai compris et c'est l'essentiel
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 66 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
