Aide Analyse

[w79exz73]

Bonjour,
J'aurai besoin d'aide pour un exercice :
Résoudre l’équation différentielle suivante avec les conditions initiales : y(0)=1 ,y'(0)=1 : y''-2y'+y=e^x x

J'ai réussi à trouver la solution générale (r-1)²=0 donc solution unique r=1 donc racine double : y=(At+B)e^t

Mais je n'arrive pas à trouver la solution particulière, j'ai fait (à partir de la je ne suis pas sûr):
q=ax²+bx+c
q'=2ax+b
q"=2a

J'ai m de e^mx qui vaut 1 (racine double de r donc deg q= 3?).

Ensuite je suis bloqué

merci d'avance

[tournesol]

Que veut dire e^xx ??

[w79exz73]

x.e^x

[phyelec]

Bonjour,

Ok pour la solution générale.
Le second membre est de la forme P(x)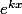 , et ici k=1 est racine double de l'équation caractéristique, il existe une solution particulière de Q(x) 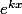avec deg(Q)=deg(P) + 2.

Dans ce vous avez essayé, le degré est 2 et l'exponentielle est absente .
on a P(x)=x donc deg(P)=1, donc deg(Q)=3, vous pourriez essayer par exemple pour solution particulière qui est un polynôme de degré 3.

[w79exz73]

D'accord donc y=ax^3e^x
y'=ax^3e^x+3ax²e^x
y''=ax^3e^x+6axe^x+6ax²e^x

x.e^x = (ax^3e^x)-2(ax^3e^x+3ax²e^x)+(ax^3e^x+6axe^x+6ax²e^x)

Ensuite on doit remplacer "a" par 1 et résoudre ?

[tournesol]

il faut mettre en facteur e^x

[w79exz73]

Sa change quelque chose entre la solution
y=(ax^3+bx²+cx+d)e^x et y=ax^3e^x

[tournesol]

je mets en facteur e^x dans l'avant dernière ligne de ton message posté à 1h15 , après réduction de la partie droite : .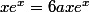
La valeur de a est évidente .

[w79exz73]

Ce qui nous donne la solution particulière ((x^3)/6)e^x

Solution générale : ((x^3)/6)e^x + (Ax+B)e^x
Donc y(0)=B=1
y'=((18x²e^x+6x^3e^x)/6²)+Ae^x+(Ax+B)e^x
Donc y'(0)=A+B=1
A=0

Donc la solution : y=((x^3e^x)/6)+e^x

C'est bien ça?
Et pourquoi peut-on remplacer (ax^3+bx²+cx+d)e^x par ax^3e^x ?

[phyelec]

[Bonjour,

La solution est bien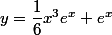

Votre question : Et pourquoi peut-on remplacer (ax^3+bx²+cx+d)e^x par ax^3e^x ?

On aurait pu prendre au lieu de , en faisant les calculs on aurait trouvé b=c=d=0 (faites les calculs pour vous en convaincre). Je m'en doutais un peu c'est pour cela que je vous ai proposé d'essayer comme solution particulière. Si cela n'avait pas fonctionné il aurait fallu prendre et déterminer a,b,c,d.

[w79exz73]

J'ai essayé de résoudre cela me donne 2 inconnues : xe^x=(e^x)(6ax+2b)
a=1/6 et b=x/2
C'est une autre solution particulière qui marche aussi : (((x^3)/6)+(x^3)/2)e^x

y=(((x^3)/6+(x^3)/2)e^x)+(Ax+B)e^x

merci à vous

[phyelec]

Bonjour,

Ok pour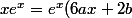 , mais après vous vous trompez dans le calcul.

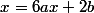vous pouvez simplifier par , vous avez alors soit 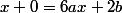, il faut avoir l'égalité de chaque terme de puissance de x , donc :
x=6ax
0=2b

ce qui donne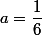 et b=0

[w79exz73]

Re bonjour,
J'ai une dernière question j'aimerai savoir l'ensemble du polynome de droite est dans C et l'équation a gauche est dans R3, et l'ensemble d'arrivé est dans R?

merci