Recurrence Linéaire

[Timothé]

Bonjour à tous,
je bloque sur un problème depuis quelques jours et je ne parviens pas à trouver a solution.
Je dois chercher les suites géométriques u = (un)n∈N qui appartiennent à E, et justifier qu’elles
forment un sous-espace vectoriel de E de dimension 1 et en donner une base.
E étant l’ensemble des suites u = (un)n∈N qui vérifient la relation de récurrence : ∀n∈N, un+2 =4un+1 −4un.
Juste avant j'ai du factoriser un polynôme ayant pour racine 2 : (x-2)(x-2). J'imagine que cela à un lien avec les racines trouvées.
Pour le moment l'ensemble des suites que j'ai trouvé est donc : a_n= λq^n, λ∈ℝavec q=2. Mais je n'arrive pas à montrer que cet ensemble représente un sev de E.
Je ne demande pas de réponse mais des pistes qui pourraient m'aider à avancer.
Merci d'avance !

[GaBuZoMeu]

Tu as fais le gros du boulot. Revois dans ton cours ce qu'il faut vérifier pour s'assurer qu'un sous-ensemble est un sous-espace vectoriel, si tu l'as oublié. Peux-tu nous dire ce qu'il faut faire ?

[Timothé]

Alors, vérifier que la suite nulle est inclus dans E de sorte que E soit non vide, s'assurer que la somme de deux suites de E est inclus dans E (et c'est là où je sèche) et enfin vérifier que pour un réel multipliant la suite, cette dernière reste dans E.
Mon problème est que je ne vois pas quelle autre suite prendre pour m'assurer que la somme de ces deux suites est dans E. A moins que je prenne une suite u=λ2^n et une suite v=λ'2^n ?

[GaBuZoMeu]

What else ?

[Timothé]

Nespresso ?
Plus sérieusement, u+v=(λ+λ')2^n et on reconnait la suite géométrique ? Et pour λ+λ'∈ℝalors u+v inclus dans E ?

[GaBuZoMeu]

Tu devrais parenthéser correctement (sinon, ça ne va pas le faire).

[Timothé]

Oui complètement c'est une erreur d'inattention, j'ai modifié mon message.
Maintenant comment puis-je interpréter (λ+λ') ? Définir leur domaine de définition suffit-il ?

Ensuite pour la stabilité par multiplication externe on choisit un α∈ℝ, on regarde αa_n qui donne α(λ2^n) or (λ2^n) est inclus dans E et ceci justifie la stabilité par multiplication externe ?
Merci pour vos réponses.

[GaBuZoMeu]

Pourquoi veux-tu "interpréter" ???
C'est une somme de deux réels, ça fait un réel, point barre.

Tu n'as pas l'air très sûr de toi sur le coup.

En fait, les solutions de l'équation de récurrence qui sont des suites géométriques forment une droite vectorielle dans l'espace des suites, engendrée par la suite . Les "vecteurs" de cette droite vectorielle sont les multiples scalaires de . La vérification que est bien un sous-espace vectoriel est triviale, peut-être tellement triviale que c'est ça qui te gêne ?

[Timothé]

Oui c'est ça qui me gêne, je pensais qu'il fallait aller beaucoup plus loin dans la recherche car j'ai l'habitude de travailler avec des sev qui ne sont pas des suites et il faut pousser un poil plus la recherche.

En tout cas merci beaucoup.

Pour ce qui est de la base de ce sev, j'ai l'habitude de travailler avec (par exemple) un vecteur de ce sev. Exemple j'ai un sev F={(x,y,z)∈ℝ^3, x - 3 y + z = 0}, j'extrais x=3y-z, et je prends par exemple u=(3y-z, y, z) etc...

Ici dans le cas des suites je me retrouve un peu perdu car mon sev est donc apriori E1={∀n∈N ∀λ∈ℝ, λ2^n} et je ne vois pas directement comment je pourrai en extraire une base ?

[GaBuZoMeu]

Il ressort de ce que tu écris que tu ne comprends la nature de l'espace vectoriel avec lequel tu travailles.

Tu as eu jusqu'à présent l'habitude de travailler avec les espaces vectoriels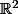 , 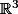etc. dont les éléments se voient bien comme des vecteurs, au sens habituel (géométrique).
Maintenant, dans l'étude de l'algèbre linéaire, il te faut faire un saut conceptuel. Les éléments d'un espace vectoriel peuvent être n'importe quoi, ce qui compte c'est le fait qu'on sache faire sur eux deux opérations :
- l'addition,
- la multiplication par un scalaire,
opérations dont on demande certaines propriétés exprimées dans les axiomes d'espace vectoriel.
Par exemple, on peut considérer des espaces vectoriels dont les éléments (les "vecteurs") sont des fonctions à valeurs dans : on sait additionner de telles fonctions, on sait les multiplier par des scalaires. On peut considérer des espaces vectoriels dont les éléments sont des polynômes, des matrices ...
Dans ton exercice on a des espaces vectoriels dont les éléments sont des suites. On sait additionner deux suites : la suite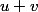 est la suite des 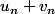. On sait multiplier une suite par un scalaire : la suite 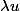est la suite des .

J'insiste : les éléments de l'espace vectoriels, les "vecteurs", sont ici des suites. Ton écriture E1={∀n∈N ∀λ∈ℝ, λ2^n} ne veut rien dire !
Il vaut mieux commencer par écrire en français, plutôt que de s'emmêler les pinceaux dans les symboles et les quantificateurs.
est le sous-espace des suites telles qu'il existe un réel tel que, pour tout entier naturel ,
Les éléments de , les vecteurs, sont des suites. J'insiste très lourdement, mais il faut bien que tu te rentres ça dans la tête. Sinon, tu seras complètement largué dès que tu feras de l'algèbre linéaire ailleurs que dans 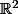ou .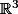
Puisque les lecteurs sont des suites, une base d'un espace vectoriel de suites sera une famille de suites. Logique, non ?
Ici, pour ton , une base est juste la famille à un élément, la suite définie par pour tout entier naturel . Pour tout élément de (enfonçons le clou : le vecteur est une suite), il existe un unique scalaire (nombre réel) tel que 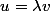. Le sous-espace est la droite vectorielle (espace vectoriel de dimension 1) engendrée par le vecteur (lequel vecteur est une suite )

[Timothé]

Oui je t'avoue que je suis un peu dépaysé avec les ev et sev de suite, c'est nouveau et étant en cours distanciel c'est plus compliqué d'assimiler les notions et poser les questions au prof.
En tout cas ton explication était clair, je t'en remercie, et je pense garder ce message dans un coin de mon cours

[GaBuZoMeu]

Avec plaisir.