Dérivabilité de arcsin (u(x))

[Math3matiqu3]

Bonsoir,



Soit , la fonction réciproque de

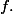
Montrer que est dérivable sur , et que

Je trouve et je trouve bel et bien
mais je ne sais pas pourquoi serait dérivable en

car n'est pas continue sur

de l'aide svp ?

[GaBuZoMeu]

Fonction réciproque de restreinte à quel intervalle et à valeurs dans quel intervalle ? Ça m'étonnerait que soit définie sur . Vérifie ton énoncé.

[Math3matiqu3]

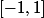
La fonction est définie dans , donc ?

En tout les cas, la fonction réciproque n'est pas définie en !

[GaBuZoMeu]

Tu pourrais commencer par étudier le domaine de définition et les variations de f, pour savoir sur quel intervalle tu la considères.

[Math3matiqu3]

ça a été fait un peu plus tôt dans l'énoncé, est positive et est strictement croissante sur son domaine de définition.

[GaBuZoMeu]

Et c'est dans l'énoncé que tu as lu "Montrer que est dérivable sur " ?
Quand tu te décideras à donner correctement et suffisamment complètement l'énoncé, on pourra discuter utilement.

[Ben314]

Salut,

ça a été fait un peu plus tôt dans l'énoncé, est positive et est strictement croissante sur son domaine de définition.

C'est évident que c'est complètement faux : la fonction f est clairement 2.pi périodique donc f(0)=f(2.pi) et elle ne peut pas être strictement croissante sur son domaine de définition.