Isotrope/ écriture canonique
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 05 Mai 2020, 14:54
par GaBuZoMeu » 05 Mai 2020, 14:54
Pour l'inclusion, OK. Je tiquais juste sur la rédaction.
Donc pour tout g appartenant à

et f appartenant à

:

inclus dans
^\perp)
Tu quantifies sur des g et f qui n'apparaissent plus dans le reste de la phrase !
Je tique aussi sur la façon dont tu écris la définition du noyau. Là, il manque une quantification universelle sur le

. Il faudrait écrire
=0\})
.
Il te reste à voir que tout polynôme de degré
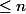
s'écrit comme somme d'un polynôme pair et d'un polynôme impair, tous deux de degrés
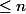
. N'est-ce pas assez évident ?
-
CorentinD
- Membre Naturel
- Messages: 57
- Enregistré le: 19 Mar 2020, 10:13
-
 par CorentinD » 05 Mai 2020, 17:46
par CorentinD » 05 Mai 2020, 17:46
GaBuZoMeu a écrit:Je tique aussi sur la façon dont tu écris la définition du noyau. Là, il manque une quantification universelle sur le . Il faudrait écrire .
Je vous remercie pour vos précisions.
Par conséquent j'en déduis que la méthode pour trouver le noyau est correcte
GaBuZoMeu a écrit:Il te reste à voir que tout polynôme de degré s'écrit comme somme d'un polynôme pair et d'un polynôme impair, tous deux de degrés . N'est-ce pas assez évident ?
Oui cela est évident mais comment l'expliquer "mathématiquement" ?

=

avec i=2p (p réel) +

avec i=2p+1
-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 05 Mai 2020, 22:02
par GaBuZoMeu » 05 Mai 2020, 22:02
Ta dernière écriture ne va pas. D'abord, un gros ennui : tu écris qu'un espace vectoriel

est égal à un polynôme

. C'est le genre de truc qui fait bondir au plafond tout correcteur, donc fait plus attention à ce que tu écris et à la nature des objets que tu manipules.
Ensuite, si tu veux indexer correctement :

où

est la partie entière de
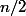
et

celle de
/2)
.
Ou alors, pour
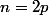

et pour
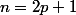

Modifié en dernier par
GaBuZoMeu le 06 Mai 2020, 10:12, modifié 1 fois.
-
CorentinD
- Membre Naturel
- Messages: 57
- Enregistré le: 19 Mar 2020, 10:13
-
 par CorentinD » 06 Mai 2020, 08:53
par CorentinD » 06 Mai 2020, 08:53
Oui excusez-moi ! Je reprends :
Pour tout
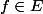
un polynôme de degré
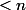
.
On a montré que tout polynôme de degré
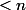
s'écrit comme somme d'un polynôme pair

et d'un polynôme impair

, tous deux de degrés
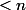
Donc

Maintenant si je veux la signature de
)
D'après le théorème d'inertie de Sylvester :

Or on a montré que q est non-dégénérée alors
= dim(E)=n+1)
Donc
= p+ + p- = n+1)
On sait que
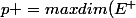; E^+ \subset E tel que q|E^+)
(restreint) soit définie positive}
J'ai donc envie de dire que
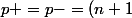/2)
Mais je ne suis pas sûr
-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 06 Mai 2020, 09:47
par GaBuZoMeu » 06 Mai 2020, 09:47
Il faudrait déjà que (n+1)/2 soit entier ...
Réfléchis mieux. Tu connais un sous-espace sur lequel la restriction de la forme quadratique est définie positive, un autre sur lequel elle est définie négative et ces deux sous-espaces sont supplémentaires.
-
CorentinD
- Membre Naturel
- Messages: 57
- Enregistré le: 19 Mar 2020, 10:13
-
 par CorentinD » 06 Mai 2020, 10:09
par CorentinD » 06 Mai 2020, 10:09
Le sous-espace sur lequel la restriction de la forme quadratique est définie positive est

et l'autre où elle est définie négative est

Ces deux sous espaces sont supplémentaires donc :
=dim(E^+)+dim(E^-))
Donc
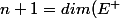+dim(E^-))
Mais je n'arrive pas à "généraliser" avec des exemples par exemple si f1 un polynôme et

alors s
=(1,1))
,

alors
=(0,2))
-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 06 Mai 2020, 10:19
par GaBuZoMeu » 06 Mai 2020, 10:19
Bon. Deux moyens de s'en sortir :
1°) Il y a un résultat que tu as peut-être dans ton cours : si
)
est la signature de la forme quadratique

, alors

(resp.

) est le maximum des dimensions des sous-espaces sur lesquels

est définie positive (resp. négative). C'est souvent comme cela qu'on démontre le théorème d'inertie de Sylvester.
2°) Tu as démontré que le sous-espace des impairs est contenu dans l'orthogonal de celui des pairs. Maintenant tu peux prendre une base orthogonale du sous-espace des pairs, une base orthogonale du sous-espace des impairs et ... tu vois quoi faire ?
-
CorentinD
- Membre Naturel
- Messages: 57
- Enregistré le: 19 Mar 2020, 10:13
-
 par CorentinD » 06 Mai 2020, 10:35
par CorentinD » 06 Mai 2020, 10:35
GaBuZoMeu a écrit:1°) Il y a un résultat que tu as peut-être dans ton cours : si (p,n) est la signature de la forme quadratique , alors (resp. ) est le maximum des dimensions des sous-espaces sur lesquels est définie positive (resp. négative). C'est souvent comme cela qu'on démontre le théorème d'inertie de Sylvester.
C'est exactement comme ça que j'ai essayé de faire mais j'avais peut être mal exprimé mon idée !
Mais je ne comprends pas comment on peut écrire le maximum des dimensions des sous-espaces sur lesquels est définie positive parce que cela change pour chaque polynôme...
A moins que l'on note sg(q)=(p=maximum des dimensions des sous-espaces sur lesquels q est définie positive, n=maximum des dimensions des sous-espaces sur lesquels q est définie négative) et que l'on s'arrête là
-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 06 Mai 2020, 11:00
par GaBuZoMeu » 06 Mai 2020, 11:00
Mais je ne comprends pas comment on peut écrire le maximum des dimensions des sous-espaces sur lesquels est définie positive parce que cela change pour chaque polynôme...
Je ne comprends absolument rien à cette phrase. Peux-tu expliquer ? Que veut dire "cela change pour chaque polynôme" ? Qu'est-ce qui change ? La dimension du sous-espace des polynômes pairs ?
Reprenons. Tu cherches la signature (s,t) de la forme quadratique q. Puisque q est non dégénérée, tu sais que s+t = n+1. Tu sais que s (resp. t) est le maximum des dimensions de sous-espaces sur lesquels q est définie positive (resp. négative).
Tu connais un sous-espace sur lequel q est définie positive : celui des polynômes pairs. Quelle est sa dimension ?
Tu connais un sous-espace sur lequel q est définie négative : celui des polynômes impairs. Quelle est sa dimension ?
Conclusion ?
-
CorentinD
- Membre Naturel
- Messages: 57
- Enregistré le: 19 Mar 2020, 10:13
-
 par CorentinD » 06 Mai 2020, 11:18
par CorentinD » 06 Mai 2020, 11:18
GaBuZoMeu a écrit:Je ne comprends absolument rien à cette phrase. Peux-tu expliquer ? Que veut dire "cela change pour chaque polynôme" ? Qu'est-ce qui change ? La dimension du sous-espace des polynômes pairs ?
Oui. En fait, je n'arrive pas à trouver une expression unique pour la dimension du sous-espace des polynômes pairs.
Si je note m le degré du polynôme donc
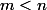
Si m est pair, la dimension est m/2 +1. (pour E^+)
Si m est impair, la dimension est (m+1)/2.
Mais je n'arrive pas à obtenir une expression unique, j'imagine il faut utiliser la partie entière mais je n'y arrive quand même pas
GaBuZoMeu a écrit: Quelle est sa dimension ?
C'est ça que je cherche et quand j'ai trouvé leur dimension alors
=(dimE^+,dimE^-))
-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 06 Mai 2020, 13:58
par GaBuZoMeu » 06 Mai 2020, 13:58
Mais qu'est-ce que tu racontes ?
Le sous-espace des polynômes pairs ne dépend pas d'un polynôme !
Pour trouver sa dimension, il vaut mieux distinguer le cas où

(le

de

) est pair et la cas où il est impair.
Ça ne devrait pas être si sorcier que ça de trouver sa dimension, on t'en donne en fait une base dans la définition de polynôme pair.
Alors si
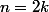
, quelle est la dimension du sous-espace des polynômes pairs ? du sous-espace des polynômes impairs ?
Et si
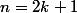
, quelle est la dimension du sous-espace des polynômes pairs ? du sous-espace des polynômes impairs ?
-
CorentinD
- Membre Naturel
- Messages: 57
- Enregistré le: 19 Mar 2020, 10:13
-
 par CorentinD » 06 Mai 2020, 14:11
par CorentinD » 06 Mai 2020, 14:11
GaBuZoMeu a écrit:une base dans la définition de polynôme pair.
Une base c'est
)
GaBuZoMeu a écrit:Alors si n=2k , quelle est la dimension du sous-espace des polynômes pairs ? du sous-espace des polynômes impairs ?
Alors dim(E)=n+1=(2k)+1=2k+1
Alors la dimension du sous-espace des polynomes pairs est k/2+1
La dimension du sous espace des polynomes impairs est k/2
GaBuZoMeu a écrit:Et si n=2k+1, quelle est la dimension du sous-espace des polynômes pairs ? du sous-espace des polynômes impairs ?
La dimension du sous-espace des polynomes pairs est (k+1)/2
La dimension du sous-espace des polynomes impairs est (k+1)/2
-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 06 Mai 2020, 14:36
par GaBuZoMeu » 06 Mai 2020, 14:36
Encore une faute d'étourderie. Fais attention !!!
-
CorentinD
- Membre Naturel
- Messages: 57
- Enregistré le: 19 Mar 2020, 10:13
-
 par CorentinD » 06 Mai 2020, 14:58
par CorentinD » 06 Mai 2020, 14:58
Ah oui ...
J'avais oublié que le polynôme est de degré maximal strictement inférieur à n
Donc je refais :
pour n=2k
Alors la dimension du sous-espace des polynomes pairs est k/2
La dimension du sous espace des polynomes impairs est k/2
Pour n=2k+1
La dimension du sous-espace des polynomes pairs est (k+1)/2
La dimension du sous-espace des polynomes impairs est (k-1)/2
-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 06 Mai 2020, 15:14
par GaBuZoMeu » 06 Mai 2020, 15:14
1°) Tu refais la même faute d'étourderie avec tes k/2 !
2°) J'ai toujours vu que
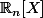
désignait l'espace des polynômes de degré inférieur ou égal à

, et pas de degré strictement inférieur à

.
-
CorentinD
- Membre Naturel
- Messages: 57
- Enregistré le: 19 Mar 2020, 10:13
-
 par CorentinD » 06 Mai 2020, 15:22
par CorentinD » 06 Mai 2020, 15:22
Autant pour moi !
Oui en fait je prends dans ma tete n=k et pas de 2k ...
Je refais :
pour n=2k
Alors la dimension du sous-espace des polynomes pairs est k+1
La dimension du sous espace des polynomes impairs est k
Et par logique on retrouve que dim(E)=2k+1 !
Pour n=2k+1
La dimension du sous-espace des polynomes pairs est k+1
La dimension du sous-espace des polynomes impairs est k+1
Et ici dim(E)=n+1=(2k+1)+1=2k+2 (je retrouve bien ça !)
-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 06 Mai 2020, 15:29
par GaBuZoMeu » 06 Mai 2020, 15:29
Ouf ! Maintenant, peux-tu revenir à la signature ?
-
CorentinD
- Membre Naturel
- Messages: 57
- Enregistré le: 19 Mar 2020, 10:13
-
 par CorentinD » 06 Mai 2020, 17:20
par CorentinD » 06 Mai 2020, 17:20
En effet, je crois que je me suis trompé avant parce que si je prends :
n=10 : alors dim(E^+)=6 et dim (E^-)=6
En fait depuis le début j'oublie de compter le x^1 pour E^-1
Mais du coup j'ai plus que dimE=dimE^+ +dimE^- ...
Pareil si je fais n=11: alors dim(E^+)=6 et dim(E^-)=7 ...
Après peut être que le X^0 il ne faut pas le compter et si c'est ça je dois enlever moins 1 à tous mes résultats ! Mais du moins je trouverai que
pour n=2k
Alors la dimension du sous-espace des polynomes pairs est k
La dimension du sous espace des polynomes impairs est k
Pour n=2k+1
La dimension du sous-espace des polynomes pairs est k
La dimension du sous-espace des polynomes impairs est k+1
-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 06 Mai 2020, 18:28
par GaBuZoMeu » 06 Mai 2020, 18:28
Tu as l'air complètement à l'ouest.
Prenons
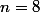
. Une base de l'espace est
)
.
Une base du sous-espace des pairs ? Une base du sous-espace des impairs ?
On recommence ensuite avec
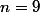
.
-
CorentinD
- Membre Naturel
- Messages: 57
- Enregistré le: 19 Mar 2020, 10:13
-
 par CorentinD » 06 Mai 2020, 18:37
par CorentinD » 06 Mai 2020, 18:37
Une base du sous-espace pair est (
)
donc la dimension de cette base est égale à 5
Une base du sous-espace des impairs est
)
donc la dimension est 5
Pour n=9,
Une base du sous-espace pair est
)
donc de dimension 5
Une base du sous-espace des impairs est
)
donc de dimension 6
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 51 invités
et f appartenant à
:
inclus dans
