Integrale a parametre et domination

[Ririyeman]

Saluuut
Je dois démontrer qu'une fonction definie par une integrale est continue donc trouver une domination mais ça me parait juste pas possible ( apres avoir regarder sur divers traceur de courbe) ma "suite" de fonction a l'air de diverger :
voici la bête F(t)=integrale 0 - inf(f(x,t)) avec f(x,t)=ln(1+tx^2)/(1+x^2)

voila voila j'ai pas réussi a trouver une domination de dépendant pas de t si vous avez quelques indication indice je dis pas non merci d'avoir lu bizou

[Ben314]

Salut,

Un petit "rappel" : être continue, c'est une propriété locale.
Pour montrer qu'une fonction est continue sur un intervalle il suffit de montrer que pour tout 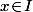il existe un voisinage 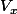contenant sur lequel la fonction est continue.

[Ririyeman]

Je ne comprend pas en quoi le fait que la continuité soit une propriété locale puisse m aider ici tu veux dire que je peux trouver plusieurs domination pour des sous intervalle de mon intervalle ? Si c est le cas j arrive toujours à quelque chose qui dépend de mon t ..