Bonjour,
voici mon exercice : "Soit

la distribution construite sur la fonction
=h_0(x)h_0(y))
où
=1)
si
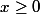
et
=0)
si
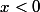
(c'est la fonction échelon). En utilisant la théorie des distributions, calculer

et en déduire
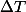
."
J'ai commencé à résoudre l'exercice :
, \quad <\frac{\partial T}{\partial x},\varphi>=-<T,\frac{\partial \varphi}{\partial x}>=-\int_0^{+\infty}\int_0^{+\infty}\frac{\partial \varphi}{\partial x}(x,y)dxdy)
-\varphi(0,y))dy= \int_0^{+\infty}\varphi(0,y)dy= \int_0^{+\infty} \int_{-\infty}^{+\infty}\delta_0(x)\varphi(x,y)dxdy=\int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty}\delta_0(x)h_0(y)\varphi(x,y)dxdy)
On peut donc conclure que
 \mapsto \delta_0(x)h_0(y))
(en faisant l'abus d'identifier une distribution à sa fonction).
De même, je trouve que
 \mapsto \delta_0(y)h_0(x))
.
En revanche, pour les dérivées d'ordre 2, je n'aboutis pas :
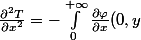dy)
mais je n'arrive pas à aller plus loin pour "enlever" la dérivée partielle...
Voilà, si quelqu'un voit comment faire, je suis preneur.... merci beaucoup !
