DM de maths (matrice, diagonalisation)
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
julie0407
- Membre Naturel
- Messages: 15
- Enregistré le: 13 Avr 2020, 16:34
-
 par julie0407 » 25 Avr 2020, 17:43
par julie0407 » 25 Avr 2020, 17:43
Bonjour tout le monde !
J'ai un exercice à rendre sur la diagonalisation d'une matrice 2x2. On me demande de montrer que :
A:

est diagonalisable.
Je commence par modifier la matrice : A=

Après je sais qu'il faut commencer par calculer son polynôme caractéristique :
Xi(A) =
 + (ab-c^2))
puis Δ=
)
Mais je vois pas comment faire après...
Merci de votre réponse !
Modifié en dernier par
julie0407 le 25 Avr 2020, 18:29, modifié 1 fois.
-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 25 Avr 2020, 17:51
par GaBuZoMeu » 25 Avr 2020, 17:51
Ton énoncé ne doit pas être vraiment tel que tu le dis. Peux-tu donner l'énoncé exact ?
-
julie0407
- Membre Naturel
- Messages: 15
- Enregistré le: 13 Avr 2020, 16:34
-
 par julie0407 » 25 Avr 2020, 18:26
par julie0407 » 25 Avr 2020, 18:26
Voici l'énoncé : Soient a,b,c des nombres r´eels quelconques. Montrer que la matrice A est diagonalisable.

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 25 Avr 2020, 19:02
par Sa Majesté » 25 Avr 2020, 19:02
Donc ça fait
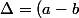^2 + 4c^2)
-
julie0407
- Membre Naturel
- Messages: 15
- Enregistré le: 13 Avr 2020, 16:34
-
 par julie0407 » 25 Avr 2020, 19:10
par julie0407 » 25 Avr 2020, 19:10
Effectivement (^^") Merci !
-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 25 Avr 2020, 21:01
par GaBuZoMeu » 25 Avr 2020, 21:01
OK. Le "réel" est important.
-
julie0407
- Membre Naturel
- Messages: 15
- Enregistré le: 13 Avr 2020, 16:34
-
 par julie0407 » 26 Avr 2020, 13:53
par julie0407 » 26 Avr 2020, 13:53
Bonjour, J'ai calculé les racines (je trouve x1 = a+c et x2 = b-c) cependant quand je remplace X par le x1 puis x2, je ne trouve pas l'équation égale à 0.
Si vous pourriez m'aider !
Merci !
-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 26 Avr 2020, 14:21
par GaBuZoMeu » 26 Avr 2020, 14:21
Les racines de quoi ??
Tu as ton polynôme caractéristique, tu en as calculé le discriminant.
Quand est-ce que le polynôme caractéristique a deux racines réelles distinctes ? Que peut-on dire alors de la diagonalisabilité de la matrice ?
Quand-est-ce que le polynôme caractéristique a deux racines réelles confondues ? Que se passe-t-il alors pour la matrice ?
Le polynôme caractéristique peut-il avoir des racines complexes conjuguées non réelles ?
-
julie0407
- Membre Naturel
- Messages: 15
- Enregistré le: 13 Avr 2020, 16:34
-
 par julie0407 » 26 Avr 2020, 14:31
par julie0407 » 26 Avr 2020, 14:31
Le polynôme a 2 racines distinctes lorsque delta est supérieur à 0, possède une racine confondu lorsque delta est égal à 0 et a des racines complexes quand delta est inférieur à 0.
Quand le polynôme possède 2 racines, la matrice est alors diagonalisable ? et que si le polynôme possède en possède qu'une seule (confondue) elle ne l'est pas ?
-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 26 Avr 2020, 14:43
par GaBuZoMeu » 26 Avr 2020, 14:43
Qu'as-tu dans ton cours comme condition suffisante de diagonalisabilité ?
Que sont les racines du polynôme caractéristique ? Pourquoi les cherches-tu ?
-
julie0407
- Membre Naturel
- Messages: 15
- Enregistré le: 13 Avr 2020, 16:34
-
 par julie0407 » 26 Avr 2020, 15:04
par julie0407 » 26 Avr 2020, 15:04
Les conditions pour que A soit diagonalisable sont :
-que la dim(A) soit égale au nombre de racine
-que sur la diagonale de D, on retrouve les racines avec des 0 autour
Je recherche les racines pour pouvoir trouver les vecteurs propres de A puis exprimer P,
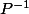
et D tel que D=
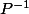
AP
-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 26 Avr 2020, 15:14
par GaBuZoMeu » 26 Avr 2020, 15:14
Je te conseille de revoir la formulation pour la diagonalisabilité.
N'as-tu pas un résultat qui dit que si A (de taille n) a n valeurs propres distinctes, alors A est diagonalisable (condition suffisante de diagonalisabilité) ?
-
julie0407
- Membre Naturel
- Messages: 15
- Enregistré le: 13 Avr 2020, 16:34
-
 par julie0407 » 26 Avr 2020, 15:19
par julie0407 » 26 Avr 2020, 15:19
La taille de A n'est-elle pas égale à sa dimension ?
-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 26 Avr 2020, 15:32
par GaBuZoMeu » 26 Avr 2020, 15:32
Je préfère ne pas parler de dimension pour une matrice, vu que le terme dimension en algèbre linéaire est employé pour les espaces et sous-espaces vectoriels. Mais c'est un détail. Je répète ma question : as-tu oui ou non ce résultat dans ton cours ?
-
julie0407
- Membre Naturel
- Messages: 15
- Enregistré le: 13 Avr 2020, 16:34
-
 par julie0407 » 26 Avr 2020, 15:35
par julie0407 » 26 Avr 2020, 15:35
Oui
-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 26 Avr 2020, 15:38
par GaBuZoMeu » 26 Avr 2020, 15:38
Eh bien applique-le ici et réponds à mes questions :
Quand est-ce que le polynôme caractéristique a deux racines réelles distinctes ? Que peut-on dire alors de la diagonalisabilité de la matrice ?
Quand-est-ce que le polynôme caractéristique a deux racines réelles confondues ? Que se passe-t-il alors pour la matrice ?
Le polynôme caractéristique peut-il avoir des racines complexes conjuguées non réelles ?
J'attends des réponses qui parlent de a,b,c.
-
julie0407
- Membre Naturel
- Messages: 15
- Enregistré le: 13 Avr 2020, 16:34
-
 par julie0407 » 03 Mai 2020, 15:39
par julie0407 » 03 Mai 2020, 15:39
J'ai eu des indications par mon prof de maths, merci de votre aide.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 34 invités
