Forme bilinéaire
43 messages
- Page 2 sur 3 - 1, 2, 3
Re: Forme bilinéaire
Le noyau de gauche  On a que la coordonnées de u est ei et la coordonnées de v est la somme de yjfj
On a que la coordonnées de u est ei et la coordonnées de v est la somme de yjfj
Re: Forme bilinéaire
Si i est différent de u alors (ei,w)=0 pour tout w appartient a v alors ei appartient au noyau gauche
Si i=u alors
Donc n’appartient pas au noyau de gauche
Re: Forme bilinéaire
Tu as effectivement beaucoup de mal à t'exprimer clairement. Mais c'est encore pire avec les formules.
Pourtant, il semble bien que tu arrives à voir ce qui se passe.
Un vecteur de
de  est dans le noyau gauche de
est dans le noyau gauche de  si et seulement si pour tout vecteur
si et seulement si pour tout vecteur  de
de  ,
, 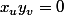 . En particulier, pour
. En particulier, pour 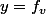 , on doit avoir
, on doit avoir 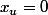 . Et réciproquement, si
. Et réciproquement, si 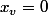 on a bien
on a bien 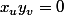 pour tout vecteur
pour tout vecteur  de
de  . Le noyau gauche de
. Le noyau gauche de  est donc le sous-espace des vecteurs de
est donc le sous-espace des vecteurs de  dont la coordonnées n°
dont la coordonnées n°  est nulle.
est nulle.
Pourtant, il semble bien que tu arrives à voir ce qui se passe.
Un vecteur
Re: Forme bilinéaire
Et pour le noyau droit c’est donc le sous espace vectoriel des vecteur V dont la coordonnée v est nulle
Et pour la question d)
Je montre que la famille est libre on pose appartenant à k tq
appartenant à k tq  +…+
+…+  =0
=0
On applique sur ei On a donc
+ \lambda_2\epsilon_{2}(ei)) +…+
+…+) +…+
+…+ ) =0
=0
On obtient) =0
=0
) =1 et
=1 et  =0
=0
Donc libre
Et pour la question d)
Je montre que la famille est libre on pose
On applique sur ei On a donc
On obtient
Donc libre
Re: Forme bilinéaire
Génératrice ?
On pose B appartient à B(U,V)
B(X,Y)=B( )=
)= B(ei,fj) possible car bilineaire
B(ei,fj) possible car bilineaire
On peut remplacer par
par )
Donc B est génératrice de B(U,V)
On pose B appartient à B(U,V)
B(X,Y)=B(
On peut remplacer
Donc B est génératrice de B(U,V)
Re: Forme bilinéaire
Réponse :
1) j'ai décrit le noyau gauche. À partir de là, j'estime qu'en trouver une base est à peu près trivial.
2) pour la liberté, ça ne va pas. Qui sont tes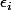 ???
???
3) pour la génération, OK, sauf que tu écris "B est génératrice". Tu ne fais pas assez attention à ce que tu écris.
1) j'ai décrit le noyau gauche. À partir de là, j'estime qu'en trouver une base est à peu près trivial.
2) pour la liberté, ça ne va pas. Qui sont tes
3) pour la génération, OK, sauf que tu écris "B est génératrice". Tu ne fais pas assez attention à ce que tu écris.
Re: Forme bilinéaire
Si B est génération alors B est une base de B(U,V)
Est ce que c’est affirmation est suffisante ou faut il aussi montrer la liberté ?
Est ce que c’est affirmation est suffisante ou faut il aussi montrer la liberté ?
Modifié en dernier par Mark236 le 23 Avr 2020, 15:06, modifié 1 fois.
Re: Forme bilinéaire
Et pour le noyau droit c’est donc le sous espace vectoriel des vecteur V dont la coordonnée v est nulle
Et pour la question d)
Je montre que la famille est libre on pose appartenant à k tq
appartenant à k tq  +…+
+…+  =0
=0
On applique sur (ei,fj )On a donc
+ \lambda_2\epsilon_{2,2}(ei,fj )) +…+
+…+) +…+
+…+ ) =0
=0
On obtient) =0
=0
) =1 et
=1 et  =0
=0
Donc libre
Et pour la question d)
Je montre que la famille est libre on pose
On applique sur (ei,fj )On a donc
On obtient
Donc libre
Re: Forme bilinéaire
Tu vois à peu près, mais tu te prends les pinceaux dans les notations et à la fin ce que tu écris ne va toujours pas.
Re: Forme bilinéaire
On applique sur (ei,fj )On a donc
+ \lambda_2\epsilon_{2,2}(ei,fj )) +…+
+…+) +…+
+…+ ) =0
=0
On obtient 0+0+…+1 +…+0 =0 donc
+…+0 =0 donc 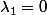 et
et 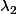 =0…
=0…
Donc libre
On obtient 0+0+…+1
Donc libre
Modifié en dernier par Mark236 le 25 Avr 2020, 03:21, modifié 1 fois.
Re: Forme bilinéaire
On pose ) =0 car
=0 car ) =0 et
=0 et ) Et
Et ) =1 ……
=1 ……) =0
=0
Soit fixé
fixé
Si i= et j
et j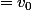 alors
alors ) =(0.e1+…1
=(0.e1+…1 +…+0.en)(0.f1+…1
+…+0.en)(0.f1+…1 +…+0.fn)=1
+…+0.fn)=1
Si i différent de et v différent de
et v différent de  alors
alors ) =0
=0
Soit
Si i=
Si i différent de
Re: Forme bilinéaire
Tu te mélanges encore les pinceaux. Il ne faut pas prendre les  , mais tous les
, mais tous les  .
.
Re: Forme bilinéaire
Faut-il que j’écrive ?
Soit fixé
fixé
Si i= et j
et j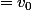 alors
alors ) =(0.e1+…1
=(0.e1+…1 +…+0.en)(0.f1+…1
+…+0.en)(0.f1+…1 +…+0.fn)=1
+…+0.fn)=1
Si i différent de et v différent de
et v différent de  alors
alors ) =0
=0
On a soit fixé
fixé
Je montre que la famille est libre on pose appartenant à k tq
appartenant à k tq  +…+
+…+  =0
=0
On applique sur (ei,fj )On a donc
+ \lambda_2\epsilon_{u_0,v_0}(ei,fj )) +…+
+…+) +…+
+…+ ) =0
=0
On obtient si i différent de et si j différent de
et si j différent de  alors
alors ) =0
=0
si i= et j=
et j= alors
alors
) =1 et
=1 et  =0
=0
Donc libre
Soit
Si i=
Si i différent de
On a soit
Je montre que la famille est libre on pose
On applique sur (ei,fj )On a donc
On obtient si i différent de
si i=
Donc libre
Re: Forme bilinéaire
Les formules que tu écris n'ont pas de sens.
Décidément, tu n'arrives pas à écrire proprement. Tu vois des choses, mais tu sembles incapable de les formuler.
Soient pour
pour 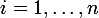 et
et  des scalaires tels que
des scalaires tels que

En particulier, pour tout et tout
et tout  , on a
, on a
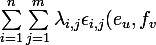 =0)
Or) vaut 1 si
vaut 1 si  et
et  et 0 sinon. L'égalité précédente donne donc
et 0 sinon. L'égalité précédente donne donc  .
.
Ceci montre que la famille des pour
pour 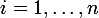 et
et  est libre.
est libre.
Décidément, tu n'arrives pas à écrire proprement. Tu vois des choses, mais tu sembles incapable de les formuler.
Soient
En particulier, pour tout
Or
Ceci montre que la famille des
43 messages
- Page 2 sur 3 - 1, 2, 3
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 53 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
