[TS] Limites de suites [Resolu]

par **boubou01** » 27 Nov 2006, 21:27

Haa c'est encore moii lol .. franchement j'ai l'impression que je suis en train de plonger en TS lol .. enfin bon a mon dernier DM j'ai obtenu un B+ ^^ .. bon bah je bloque sur ces 2 exos donc si qqun pouvait m'aider a debuter ca serait sympa .. merci :we:

par **mary123** » 27 Nov 2006, 23:59

Pour le deuxième exercice

1) tu calcule w(n+1)/w(n)=(v(n+1)-u(n+1))/(v(n)-u(n)). Tu devrais obtenir un chiffre positif : la raison de ta suite. Comme W0 est positif, ta suite est à termes positifs

b) T'aura une suite géométrique dont tu connaitra la raison. Si elle est entre -1 et 1 ta suite converge vers 0 sinon elle diverge

2) a) Tu calcule U(n+1)-U(n) et tu montre que c'est positif. A mon avis tu devrais pouvoir l'exprimer en fonction de Wn

b) V(n+1)-V(n) et tu montre que c'est négatif . A mon avis tu devrais pouvoir l'exprimer en fonction de -Wn

c) Un croissante donc Un >U0 et Vn décroissante donc Vn
3) Surement que Un et Vn sont adjacentes (une croissante une décroisssante et la limite de la différence tend vers 0 à montrer)

4) Montrer que T(n+1)-T(n)=0. La constante est égale à T0

b) Tu sais que 3Un+8Vn=T0
donc comme lim Un= lim Vn=l
3l+8l=To
donc 11l=To donc t'as l

Bonne chance

par **maturin** » 28 Nov 2006, 16:17

pour le premier
1)a)
un>0 : ça tu le démontres par récurrence simple :
montrer que: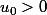

et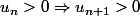

après tu calcules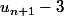

sous la forme

et tu montres que le A est négatif.

b) pareil faut utiliser la récurrence en ajoutant au passage u_n\leq6 dont tu auras besoin:
tu calcules u_1
tu supposes

et tu montres

c) là il faut reprendre le A que tu as calculé en 1)a) et grace à

le résultat devient évident.

d) pour l'inégalité c'est de la récurrence très simple grace au résultat du c)
pour la limite il suffit de faire tendre n vers +inf dans cette inégalité.

par **boubou01** » 29 Nov 2006, 19:34

Merci d'essayer de m'aider^^

Alors j'ai commencé par l'exo II .. alors pour la :

1)a.

tu calcule w(n+1)/w(n)=(v(n+1)-u(n+1))/(v(n)-u(n))

Je suis pas tres d'accord avec la technique^^ Moi j'ai juste calculer W(n+1) et je trouve 1/12(Wn) .. donc la raison est 1/12 ..

Comme W0 est positif, ta suite est à termes positifs

LoL .. je pense pas que cette justification est possible car on peut bien avoir une suite avec des termes décroissants .. enfin bon j'ai surement tort ..

b. J'ai trouvé CQFD

2)a. J'ai trouvé CQFD

b. J'ai trouvé CQFD

c. [quote]Un croissante donc Un >U0 et Vn décroissante donc Vn<

Enfin bon merci de m'avoir guidé un ptit peu deja^^

par **mary123** » 29 Nov 2006, 20:55

[quote="boubou01"]Merci d'essayer de m'aider^^

Alors j'ai commencé par l'exo II .. alors pour la :

1)a.
Je suis pas tres d'accord avec la technique^^ Moi j'ai juste calculer W(n+1) et je trouve 1/12(Wn) .. donc la raison est 1/12 ..

Oui c'est bon aussi

LoL .. je pense pas que cette justification est possible car on peut bien avoir une suite avec des termes décroissants .. enfin bon j'ai surement tort ..

Si ton w0 est positif et ta raison aussi alors ca te fait forcément une suite à termes positifs

par **boubou01** » 29 Nov 2006, 20:56

Ha ok .. en effet je suis bete sur ce coup-là^^ .. me reste plus que la recurrence donc ..

par **mary123** » 29 Nov 2006, 20:57

C'est laquelle de récurrence que t'arrives pas

par **boubou01** » 29 Nov 2006, 20:59

[quote]c.
Citation:
Un croissante donc Un >U0 et Vn décroissante donc Vn<

par **mary123** » 29 Nov 2006, 21:01

Initialisation

U0
Hérédité tu suppose que Un
U(n+1)-V(n+1)=(Un+2Vn)/3-(Un+3Vn)/4
=(4Un+8Vn-3Un-9Vn)/12
=(Un-Vn)/12
=-Wn/12
Comme Wn est à termes positifs alors U(n+1)-V(n+1) est négatif donc U(n+1)
Donc Un

[TS] Limites de suites [Resolu]

[TS] Limites de suites [Resolu]

euh pas trop de reponse a proposer mais ...

merci

Qui est en ligne