Problème de cases

[pierrelouisbourgeois]

Bonjour à tous,

Petit problème pour faire passer le temps:

On commence par écrire dans des cases une suite de 200 zéros. Puis on ajoute 1 au nombre
écrit dans chaque case, puis on ajoute 1 aux nombres d’une case sur deux (à partir de la seconde), puis on
ajoute 1 aux nombres d’une case sur 3 (à partir de la troisième) et ainsi de suite. Le jeu cesse après avoir
rajouté le dernier 1 au nombre de la 200ème case. Déterminer le nombre écrit dans la 120ème case.

Bonne journée

[GaBuZoMeu]

Si je comprends bien, la case n° k reçoit autant de 1 que k a de diviseurs ?

[pierrelouisbourgeois]

Si je comprends bien, la case n° k reçoit autant de 1 que k a de diviseurs ?

Oui

[GaBuZoMeu]

Bon, j'ai l'impression d'avoir un peu gâché l'énigme.
Pour me racheter, je la prolonge :
Est-ce que la case n°120 est celle parmi les 200 qui contient le plus grand nombre ? Sinon, quelle est cette case ?

[Idriss]

On a

On a donc

On voit que cela ne dépend pas du choix des donc mieux vaut les prendre les plus petit possible :











le max est atteint en la case

[Idriss]

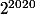
Question subsidiaire : Trouver un nombre entier naturel plus petit que avec le plus de diviseur.