Bonsoir, besoin d'aide s'il vous plaît.
Il s'agit de cette équation 1+2sinxcosx-2cos2x=0
En effet j'ai remarqué que 1+2sinxcosx=(cosx+sinx)²
(cosx+sinx)²=2cos2x de toute manière je vais me retrouver avec un cos(pi/4-x)=±√cos2x j'arrive pas à gérer la racine carrée je sais pas si c'est la bonne méthode.
Merci
Équations trigonométriques
8 messages
- Page 1 sur 1
Re: Équations trigonométriques
Salut,
Tu peux aussi tranformer 2sinx cos x en sin(2x)
Poser y=2x et te ramener à une équation du type acos y + bsin y = c
Tu peux aussi tranformer 2sinx cos x en sin(2x)
Poser y=2x et te ramener à une équation du type acos y + bsin y = c
Re: Équations trigonométriques
Ça ne marche pas dans ce cas là a=√5/5 et b=2√5/5 qui ne sont ni l'un ni l'autre cosinus ou sinus d'angle remarquable.
Re: Équations trigonométriques
Ah bon ?
Parce qu'on doit toujours tomber sur des angles remarquables ?
Parce qu'on doit toujours tomber sur des angles remarquables ?
Re: Équations trigonométriques
Je ne te suis pas.
On a bien un angle dont le cosinus vaut √5/5 et le sinus 2√5/5 donc où est le problème ?
Peu importe qu'on sache ou pas l'exprimer avec pi.
On a bien un angle dont le cosinus vaut √5/5 et le sinus 2√5/5 donc où est le problème ?
Peu importe qu'on sache ou pas l'exprimer avec pi.
Re: Équations trigonométriques
Salut,
Autre approche
1 + 2.sin(x).cos(x) - 2 cos(2x)=0
1 + sin(2x)- 2 cos(2x)=0
sin(2x) = 2.cos(2x) - 1 (1)
sin²(2x) = (2.cos(2x) - 1)²
1 - cos²(2x) = 4.cos²(2x) + 1 - 4.cos(2x)
5.cos²(2x) - 4.cos(2x) = 0
cos(2x) * (5.cos(2x) - 4) = 0
... qui permet de trouver les valeurs de cos(2x) et par (1) les valeurs correspondantes de sin(2x)
... D'en déduire les valeurs de 2x et puis de x qui sont solutions de l'équation donnée.

Autre approche
1 + 2.sin(x).cos(x) - 2 cos(2x)=0
1 + sin(2x)- 2 cos(2x)=0
sin(2x) = 2.cos(2x) - 1 (1)
sin²(2x) = (2.cos(2x) - 1)²
1 - cos²(2x) = 4.cos²(2x) + 1 - 4.cos(2x)
5.cos²(2x) - 4.cos(2x) = 0
cos(2x) * (5.cos(2x) - 4) = 0
... qui permet de trouver les valeurs de cos(2x) et par (1) les valeurs correspondantes de sin(2x)
... D'en déduire les valeurs de 2x et puis de x qui sont solutions de l'équation donnée.
Re: Équations trigonométriques
Bonjour,
ou aussi
\,cos(x)-2\,cos(2\,x)=0)
en remplaçant par
par +sin^2(x)) ,
, 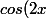) par
par -sin^2(x))
on obtient une équation du 2d degré en [ou sin(x)])
-2 sin(x) cos(x)-3 sin^2(x)=0)
d'où=...)
ou aussi
en remplaçant
on obtient une équation du 2d degré en
d'où
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 50 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
