Espérance d'une v.a.
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)

-
Ncdk
- Membre Rationnel
- Messages: 758
- Enregistré le: 30 Mar 2014, 19:10
-
 par Ncdk » 06 Avr 2020, 18:27
par Ncdk » 06 Avr 2020, 18:27
Bonjour,
Je me replonge dans un peu de mathématique mais je suis bloqué sur cet exercice.
Soit X une v.a. positive dont la loi admet une densité de probabilité. Montrer que :
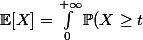 dt})
.
Début de résolution :
=1-\mathbb{P}(X< t)=1-F_X(t))
Par définition d'une densité de probabilité :
=\mathbb{P}(X\qeq t)=\int_{t}^{+\infty}{f_X(x) dx})
dt}=\int_{0}^{+\infty}{(\int_{t}^{+\infty}{f_X(x) dx})dt})
Je pense qu'en utilisant le théorème de Fubini-Tonelli, je vais pouvoir intervertir les intégrales, mais ça ne me mène nulle part. Ce n'est peut-être pas la bonne manière de faire.
Merci d'avance.
-
LB2
- Habitué(e)
- Messages: 1504
- Enregistré le: 05 Nov 2017, 16:32
-
 par LB2 » 06 Avr 2020, 18:42
par LB2 » 06 Avr 2020, 18:42
Hello,
c'est la version "à densité" du théorème de la baignoire qui existe aussi pour une v.a. discrète.
On peut utiliser une intégration par parties sur un segment et passer à la limite (proprement).

-
Ncdk
- Membre Rationnel
- Messages: 758
- Enregistré le: 30 Mar 2014, 19:10
-
 par Ncdk » 06 Avr 2020, 18:49
par Ncdk » 06 Avr 2020, 18:49
Est-ce que tu aurais un lien pour illustrer tes propos ? Je suis plus du tout dans les cours, j'ai perdu des notions sur les lois à densité et surtout l'intégration en règle générale.
-
tournesol
- Membre Irrationnel
- Messages: 1509
- Enregistré le: 01 Mar 2019, 18:31
-
 par tournesol » 06 Avr 2020, 19:24
par tournesol » 06 Avr 2020, 19:24
Le theorème de FT règle rapidement le pb.
dx)dt=\int_0^{+\infty}(\int_0^x f_X(x)dt)dx=\int_0^{+\infty}xf_X(x)dx=E(X))

-
Ncdk
- Membre Rationnel
- Messages: 758
- Enregistré le: 30 Mar 2014, 19:10
-
 par Ncdk » 07 Avr 2020, 10:52
par Ncdk » 07 Avr 2020, 10:52
Bonjour,
Merci de ta réponse ! En revanche, je ne comprends pas la première égalité et ce "changement de bornes". Je suis archi rouillé sur Fubini-Tonelli... Est-ce que tu pourrais m'éclaircir sur cette égalité ?
-
GaBuZoMeu
- Habitué(e)
- Messages: 6133
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 07 Avr 2020, 11:00
par GaBuZoMeu » 07 Avr 2020, 11:00
Tu intègres
\to f(x))
sur l'ensemble des
)
tels que
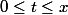
. On peut commencer par intégrer en

, ou par intégrer en

.
-
LB2
- Habitué(e)
- Messages: 1504
- Enregistré le: 05 Nov 2017, 16:32
-
 par LB2 » 07 Avr 2020, 11:49
par LB2 » 07 Avr 2020, 11:49
On peut se passer du théorème de Fubini en procédant "naïvement" avec une I.P.P (en intégrant 1 et en dérivant F), mais il faut un peu de soin lors du passage à la limite, pour justifier la convergence.
-
tournesol
- Membre Irrationnel
- Messages: 1509
- Enregistré le: 01 Mar 2019, 18:31
-
 par tournesol » 07 Avr 2020, 12:39
par tournesol » 07 Avr 2020, 12:39
Je sais plus si on peut faire une IPP avec une fonction dérivable presque partout .
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 56 invités
