Bonjour à tous. J'ai du mal à comprendre l'integration , je voudrais donc vous demander de l'aide....
Voici mon énnoncé d'exercice:
Detarminer trois nombres a,b et c tels quevpour tout nombres x different de -2 :
(x^2 -5)/(x+2)=ax+b+c/(x+2)
2. Déduisez en J= l'integrale de -1 à 6 x^2/(x-1)^2 dx.
Voilà j'espere que vous pourrez m'aider, et merci d'avance.
Intégration
9 messages
- Page 1 sur 1
Re: Intégration
Salut,
On te demande de décomposer sous la forme
sous la forme  car on sait intégrer chacun des 3 termes qui en résultent.
car on sait intégrer chacun des 3 termes qui en résultent.
Pour trouver a, b et c, plusieurs solutions.
Par exemple tu peux choisir de calculer pour 3 valeurs de x différentes.
pour 3 valeurs de x différentes.
Cela te donnera un système linéaire de 3 équations à 3 inconnues.
On te demande de décomposer
Pour trouver a, b et c, plusieurs solutions.
Par exemple tu peux choisir de calculer
Cela te donnera un système linéaire de 3 équations à 3 inconnues.
Re: Intégration
Bonjour,
ou encore :
(x² -5)/(x+2)=ax+b+c/(x+2)=
[(ax+b)(x+2)+c]/(x+2)= [ax²+x(2a+b)+(2b+c)]/(x+2)
Par identification avec (x² -5)/(x+2), on a :
a=1
2a+b=0
2b+c=-5
Soit :
a=1, b=-2 et c=-1
D'où :
(x² -5)/(x+2)=( x-2)-1/(x+2)
ou encore :
(x² -5)/(x+2)=ax+b+c/(x+2)=
[(ax+b)(x+2)+c]/(x+2)= [ax²+x(2a+b)+(2b+c)]/(x+2)
Par identification avec (x² -5)/(x+2), on a :
a=1
2a+b=0
2b+c=-5
Soit :
a=1, b=-2 et c=-1
D'où :
(x² -5)/(x+2)=( x-2)-1/(x+2)
Re: Intégration
J'ai quelquefois rencontré des lycéens à qui on avait appris la méthode de Horner pour faire la division euclidienne par 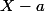 :
:

Re: Intégration
Allons-y pour d'autres méthodes !
On peut multiplier par (x+2)
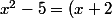(ax+b)+c)
et substituer x=-2, ce qui donne c=-1
On peut diviser par x
})
et faire tendre x vers +oo, ce qui donne a=1
On peut multiplier par (x+2)
et substituer x=-2, ce qui donne c=-1
On peut diviser par x
et faire tendre x vers +oo, ce qui donne a=1
Re: Intégration
Merci à tous pour vos réponses !
Je refléchis un peu pour la suite et je reviens vers vous si j'ai un problème ! Encore merci beaucoup
Je refléchis un peu pour la suite et je reviens vers vous si j'ai un problème ! Encore merci beaucoup
Re: Intégration
Re-bonjour à tous, pn m'a aider chez moi a teouver la solution, cependant il y a quelque choses que je n'ai pas compris.
x^2/2-2x-In(x+2) de -1 a 6 = 7/3-3In(2)
Comment on a eu ce résultat ?
x^2/2-2x-In(x+2) de -1 a 6 = 7/3-3In(2)
Comment on a eu ce résultat ?
Re: Intégration
Tu dois d'abord calculer x²/2-2x-In(x+2) pour x=6, puis lui soustraire la valeur x²/2-2x-In(x+2) pour x=-1
Je te rappelle de plus que ln1=0 et ln(a^3)=3lna
(pour ma part, je trouve 7/2 et non 7/3, mais je suppose qu'il s'agit d'une faute de frappe)
Je te rappelle de plus que ln1=0 et ln(a^3)=3lna
(pour ma part, je trouve 7/2 et non 7/3, mais je suppose qu'il s'agit d'une faute de frappe)
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 78 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
