Applications linèaires

[Hoda]

Bonjour à tous
J'arrive à cette exercice dans le TD et j'arrive pas à une solution:
Montrer que f(ker(g°f))=ker(g)interIm(f)
f appartient à L(E,F)
g appartient à L(F,G)
Merci d'avance

[GaBuZoMeu]

Tu procèdes par double inclusion en dépliant bien soigneusement les définitions.
Courage, il n'y a aucun piège caché, c'est tout bête !
Essaie, et montre nous ce que tu fais.

Soit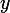 un élément de .
....
Donc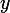 appartient à .

Et puis, attaque toi à l'autre inclusion ...

[Hoda]

D'accord merci bcp ^-^

[Mateo_13]

Bonjour,

Montrer que

1) Prends d'abord un élément puis montre que .
Ceci montre l'inclusion de gauche à droite.

2) Prends ensuite un élément et montre qu'il existe tel que .
Ceci montre l'inclusion de droite à gauche.

Cordialement,
--
Mateo.

[Hoda]

D'accord
Merci bcp ^-^

[GaBuZoMeu]

On attend ta rédaction ...