Limite x→0 (e^-x - 1) / (e^4x-1)
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
sammywey
- Membre Naturel
- Messages: 12
- Enregistré le: 02 Fév 2020, 11:39
-
 par sammywey » 01 Avr 2020, 21:01
par sammywey » 01 Avr 2020, 21:01
bonjour
j'ai besoin d'une explicaction pour le problème suivant
je ne comprends pas comment on obtient la première ligne .
d'après ce que je sais "x^-n = 1/x^n" mais je ne vois pas ça dans la résolution.
merci d'avance


-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 01 Avr 2020, 21:08
par Sa Majesté » 01 Avr 2020, 21:08
Salut,
Le numérateur et le dénominateur ont été divisés par x.
-
sammywey
- Membre Naturel
- Messages: 12
- Enregistré le: 02 Fév 2020, 11:39
-
 par sammywey » 01 Avr 2020, 21:42
par sammywey » 01 Avr 2020, 21:42
bonjour "Sa Majesté"
merci!
est ce que tu peux me confirmer que ça correspond à une loi mathématique?
que lorsqu'on à un exposant "x" , il faut diviser le terme par ce même "x" , et ensuite multiplier le tout par le "a" de "x"?
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 02 Avr 2020, 08:06
par Carpate » 02 Avr 2020, 08:06
J'espère que tu as compris le but de cette division par x du numérateur et du dénominateur .
C'est pour faire apparaître :
au numérateur : 
et en posant
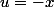
'_{u=0}=-e^0=-1) au dénominateur :
au dénominateur :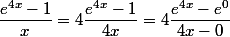
en posant

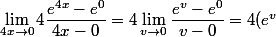'_{v=0}=4e^0=4)
-
sammywey
- Membre Naturel
- Messages: 12
- Enregistré le: 02 Fév 2020, 11:39
-
 par sammywey » 03 Avr 2020, 09:09
par sammywey » 03 Avr 2020, 09:09
mille mercis "Carpate"!
-
Black Jack
 par Black Jack » 05 Avr 2020, 08:45
par Black Jack » 05 Avr 2020, 08:45
Salut,
Autre méthode ...
lim(x-->0) [(e^(-x) - 1)/(e^(4x - 1)] est une indétermination du type 0/0 --> Règle de Lhospital.
= lim(x-->0) [(-e^(-x)/(4.e^(4x)] = -(1/4) * lim(x-->0) [e^(-5x)] = -1/4 * 1 = -1/4
A n'utiliser que si la règle de Lhospital a été enseignée ... ce qui n'est malheureusement pas toujours le cas, même en supérieur.

-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 05 Avr 2020, 13:35
par Pisigma » 05 Avr 2020, 13:35
Bonjour,
autre méthode
(e^x+e^{2x}+e^{3x}+e^{4x})})
-
tournesol
- Membre Irrationnel
- Messages: 1509
- Enregistré le: 01 Mar 2019, 18:31
-
 par tournesol » 05 Avr 2020, 19:37
par tournesol » 05 Avr 2020, 19:37
On est dans le forum du superieur et un équivalent donne -x/4x = -1/4
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 42 invités

