Cos,sin

[Hoda]

Bonjour
Comment peut montrer que
(cos(kx),sin(kx)) est une famille libre?
K compris entre 1 et 3 puis dans le cas général k compris entre 1 et n
Je pense que je dois utiliser les formules trigonométriques mais je sais pas comment le faire
Merci d'avance^-^

[tournesol]

Tu peux montrer que la famille de fonctions de … une partie de R que tu dois préciser … dans C définie par la famille des images de x : est libre dans le R-ev C .

[tournesol]

Autre aide : déterminant de Vandermonde .

[Hoda]

Merci bcp
Je veux essayer^-^

[GaBuZoMeu]

Pour démontrer qu'une famille de fonctions est libre, on dispose de beaucoup d'outils. Le but est le suivant : montrer qu'on n'a pas de relation de dépendance linéaire, c.-à-d. que si

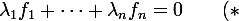alors tous les scalaires sont nuls.

On peut par exemple
1°) Évaluer la relation en points bien choisis, de façon à obtenir un système linéaire homogène en les qui n'a que la solution triviale.
2°) Dériver successivement la relation et évaluer les dérivées en un ou des point(s) bien choisi(s), pour avoir un système linéaire comme en 1°).
3°) Étudier la limite en du membre de gauche de ; si une des fonctions est dominante par rapport aux autres, alors forcément son coefficient est nul, et on peut enclencher une récurrence.
etc ....

[tournesol]

L'interet de la méthode du systeme lineaire , c'est qu'elle est valable sur tout intervalle borné .

[tournesol]

Je reconnais que l'usage des nombres complexes est une astuce marginale téléphonée par cet énoncé .
Voici une autre méthode qui peut s'appliquer à x (cos kx , sin kx , f(kx)) .
Il s'agit d'une fonction de dans .
J'applique à ces fonctions l'application linéaire qui les transforme en leur première fonction composante ie cos kx . Il suffit de démontrer que cette famille est libre (dérivations successives d'ordre pair , évaluation en n réels distincts et encore un déterminant de Vandermonde …)
Ceci étant fait , toute famille d'image libre est libre .

[GaBuZoMeu]

Je comprends l'énoncé comme demandant d'établir la liberté d'une famille d'applications à valeurs dans 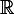: la famille dans un premier temps.

[tournesol]

Ce n'est pas ce qui est signifié dans l'enoncé qui est , selon moi , sans ambiguité .

[GaBuZoMeu]

Selon toi ...

[tournesol]

Je pense que les deux possibilités sont équivalentes (intuition non approfondie)