S'il vout plaît quelq'un peut m'aider dans cette question:
f(x)=cos(nx) . g(x)=(cos(x))^n ( càd à la puissance n)
F=vect(f), G=vect(g)
On doit montrer que F=G
(n compris entre 0 et 4)
Merci d'avance
Espace vect
4 messages
- Page 1 sur 1
Re: Espace vect
Salut,
tu as du voir comment linéariser des trucs de la forme^n) en utilisant
en utilisant =\frac{e^{ix}+e^{-ix}}{2}) puis la formule du binôme de Newton.
puis la formule du binôme de Newton.
tu as du voir comment linéariser des trucs de la forme
Re: Espace vect
Salut !
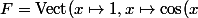, x\mapsto \cos(2x), x\mapsto \cos(3x), x\mapsto \cos(4x) )) et
et , x\mapsto \cos^2(x),x\mapsto \cos^3(x),x\mapsto \cos^4(x) )) .
.
Pour montrer que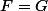 , il suffit de raisonner par "double-inclusion" i.e. montrer que
, il suffit de raisonner par "double-inclusion" i.e. montrer que 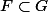 et
et 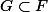 . Cela revient donc à exprimer les cinq fonctions de
. Cela revient donc à exprimer les cinq fonctions de  comme combinaison linéaire de fonctions de
comme combinaison linéaire de fonctions de  et réciproquement.
et réciproquement.
Par exemple, tu as dû voir en première que, pour tout réel ,
, = 2 \cos^2(x) -1) donc la fonction
donc la fonction ) s'exprime comme combinaison linéaire d'éléments de
s'exprime comme combinaison linéaire d'éléments de  (
(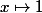 et
et ) ) donc
) donc  \in G) . Et même on en déduit que pour tout réel
. Et même on en déduit que pour tout réel  ,
,  = \frac 1 2 ( \cos(2x) +1 )) , donc
, donc ) s'exprime comme combinaison linéaire de fonctions de
s'exprime comme combinaison linéaire de fonctions de  (
(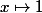 et
et ) ) donc
) donc  \in F) .
.
Les fonctions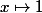 et
et ) s'exprimant trivialement comme combinaison linéaire d'éléments de
s'exprimant trivialement comme combinaison linéaire d'éléments de  et
et  , on a clairement
, on a clairement  \in G) et
et  \in F) .
.
Le plus gros du travail consiste à montrer que les fonctions) et
et ) appartiennent bien à
appartiennent bien à  , et que les fonctions
, et que les fonctions ) et
et ) appartiennent bien à
appartiennent bien à  .
.
Par exemple, montre que pour tout réel ,
,  = \frac 1 4 \cos(3x) + \frac 3 4 \cos(x)) . Je te laisse chercher pour
. Je te laisse chercher pour ) .
.
Pour "linéariser") , utilise le fait que
, utilise le fait que = \frac{e^{ix} + e^{ -ix} } 2) et utilise la formule du binôme de Newton.
et utilise la formule du binôme de Newton.

Pour montrer que
Par exemple, tu as dû voir en première que, pour tout réel
Les fonctions
Le plus gros du travail consiste à montrer que les fonctions
Par exemple, montre que pour tout réel
Pour "linéariser"
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 50 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
