État stable

[Ljb7]

Je suis entrain de faire un DM de spe maths et je bloque pouvez vous m'aider
Lors d'une greve des transports ferroviaire qui s'etale sur plusieur jours les salariés choisissent de faire grève ou pas selon les propositions suivante
30% des greviste d'une journée travaillent le jours d'après
20% des salariés travaillant un jour donnée se mettent en grève le jour suivant
Au premier jour de la grève 90% des salariés sont grévistes
On note gn la proposition de gréviste le n-ième jours de grève
1. a Traduire les données par un graphe probabiliste
b. Préciser la matrice M de transition associée à ce graphe
c. Déterminer la probabilité de gréviste le troisième jour.
2. Déterminer l'état stable associé au graphe probabiliste
3. Démontrer que pour tout n>1 on a :gn+1=0.5gn+0.2
4. On montre que (Un)défini pour tout entier n>1 par Un=gn-0.4
a. Montrer que (Un) est une suite géométrique, preciser sa raison et son premier terme
b. Exprimer Un puis t'en fonction de n
5.a. Déterminer en justifiant la limite de(gn)
b. Interpréter ce résultat


Aider moi svp j'arrive vraiment pas

[GaBuZoMeu]

Je pense que tu dois avoir dans ton cours la définition de graphe probabiliste et de matrice de transition associée à ce graphe. N'est-ce pas ?
Ici, à quoi vont correspondre les sommets du graphe ?

PS. Je trouve idiot l'habillage du problème. Mais ce n'est pas la question.

[Ljb7]

Je pense que tu dois avoir dans ton cours la définition de graphe probabiliste et de matrice de transition associée à ce graphe. N'est-ce pas ?
Ici, à quoi vont correspondre les sommets du graphe ?

PS. Je trouve idiot l'habillage du problème. Mais ce n'est pas la question.

Oui j'ai les définitions mais j'arrive pas a trouver l'état stable j'ai réussi la première question mais a partir de la deuxième je bloque

[Ljb7]

Bah je pense que les sommets c'est d'un côté les gréviste et d'un autre coté ceux qui travail

[GaBuZoMeu]

Bon réflexe. Tu peux faire le graphe, alors, et écrire la matrice.

Et pour l'état stable, je suis sûr que tu as dans ton cours la façon de le déterminer à partir de la matrice de transition. Me trompé-je ?

Peux-tu écrire la matrice de transition que tu as trouvée ? (Pour bien voir la convention d'écriture adoptée dans ton cours).

[Ljb7]

M=0.7 0.3
0.2 0.8

M^3= 0.475 0.525
0.35 0.65
Mais pour l'état stable je bloque totalement

[GaBuZoMeu]

Quelle est la définition d'état stable dans ton cours ?

[Ljb7]

Un état stable d'un graphe probabiliste de matrice de transition M est un état P tel que P=P×M

[GaBuZoMeu]

Oui. Un état stable est, comme ce nom l'indique, un état qui reste inchangé tout au long du processus. Comme le passage d'une étape du processus à la suivante est donné par la matrice de transition : , un état stable est un état qui vérifie .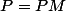
Tu sais que les états sont les où est la proportion de grévistes et celle de non grévistes, avec bien sûr 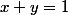(vraiment, cet habillage est ridicule, enfin ...).
Tu as la matrice de transition . Tu as donc tous les outils pour déterminer l'état stable.

[Ljb7]

D'accord merci je vais essayer merci de votre aide

[GaBuZoMeu]

Avec plaisir. N'hésite pas à revenir s'il y a un problème.