Innégalité triangulaire

[infernaleur]

Salut,
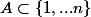
Soient , montrer qu'il existe un sous ensemble tels que:

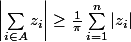
Bon courage.

[GaBuZoMeu]

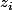
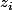
Fixons un angle et faisons la somme des dont l'argument est compris entre et (les qui tirent dans le sens indiqué par ) ; on peut minorer le module de cette somme en projetant sur la demi-droite d'angle polaire , et ensuite faire la moyenne de cette minoration quand fait tout le tour.
J'espère avoir été suffisamment obscur pour que personne ne comprenne ce que je raconte et que l'énigme n'ait pas été spoilée trop tôt.

[GaBuZoMeu]

Soient des vecteurs d'un espace euclidien de dimension 3. Montrer qu'il existe tel que .

[Queta]

Bonjour,

A = {1} convient.

[GaBuZoMeu]

Bonsoir,

N'importe quoi.

[Queta]

La norme d'un vecteur est positive donc son quart lui est inférieur au sens large.
Pareil pour le module.

Il ne manque pas des conditions sur A et n pour éviter ces cas triviaux ?

Sauf erreur de ma part.

[GaBuZoMeu]

Queta, tu persistes à raconter n'importe quoi : tu n'as pas lu, ou pas compris, l'énoncé de la question ?
Je répète la question, en français.
On a un ensemble de n vecteurs (n entier positif quelconque) dans un espace euclidien de dimension 3. Démontrer qu'il existe un sous-ensemble A de cet ensemble tel que la norme de la somme des vecteurs de A soit supérieure ou égale [à la somme] au quart de la somme des normes des n vecteurs.

[lyceen95]

je finis la phrase : ... divisée par Pi.

[GaBuZoMeu]

Nan, la phrase était erronée, mais ce n'est pas la bonne correction. Ici, on divise par 4.