Bonjour à tous il y a 3 théorèmes de mon cours que je souhaiterai mieux cerner et comprendre et dont je n'ai pas les démonstrations, auriez vous un site où je pourrai les trouver ou bien me des éléments qui me permettraient de les construire ?
Soient E et F deux K-espaces vectoriel, et f ∈ L (E, F).
1. Si E est de dimension finie et si f est surjective, alors F est de
dimension finie et dim(F) <= dim(E).
2. Si F est de dimension finie et si f est injective, alors E est de
dimension finie et dim(E) <= dim(F).
3. Si E et F sont de dimension finie, et si f est un isomorphisme,
alors dim(E) = dim(F)
je vos remercie d'avance
Théorèmes dimension
6 messages
- Page 1 sur 1
Re: Théorèmes dimension
Bonjour,
3 est une conséquence de 1 et 2.
Pour 1 et 2, on peut les démontrer en utilisant des familles génératrices et des familles libres.
Commence par prouver les lemmes suivants et ça sera plus ou moins direct :
1') les images des vecteurs d'une famille génératrice de E par une application linéaire surjective de E dans F forment une famille génératrice de F.
2') les images des vecteurs d'une famille libre de E par une application linéaire injective de E dans F forment une famille libre de F.
NB : on a aussi le théorème du rang : pour tout f appartenant à L(E,F) on a
rg(f) + dim(ker(f)) = dim(E).
3 est une conséquence de 1 et 2.
Pour 1 et 2, on peut les démontrer en utilisant des familles génératrices et des familles libres.
Commence par prouver les lemmes suivants et ça sera plus ou moins direct :
1') les images des vecteurs d'une famille génératrice de E par une application linéaire surjective de E dans F forment une famille génératrice de F.
2') les images des vecteurs d'une famille libre de E par une application linéaire injective de E dans F forment une famille libre de F.
NB : on a aussi le théorème du rang : pour tout f appartenant à L(E,F) on a
rg(f) + dim(ker(f)) = dim(E).
Re: Théorèmes dimension
Soit 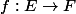 une application linéaire. Soit
une application linéaire. Soit 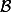 une base de
une base de  . Alors :
. Alors :
1°) est surjective si et seulement si l'image de
est surjective si et seulement si l'image de 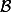 par
par  est une famille génératrice de
est une famille génératrice de  .
.
2°) est injective si et seulement si l'image de
est injective si et seulement si l'image de 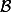 par
par  est une famille libre.
est une famille libre.
3°) est un isomorphisme si et seulement si l'image de
est un isomorphisme si et seulement si l'image de 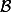 par
par  est une base de
est une base de  .
.
Ces résultats, tu les connais ? C'est la clé des résultats que tu cites, en utilisant ce que tu dois savoir sur la dimension.
Edit : le 2 est un peu délicat, parce que tu ne peux pas supposer a priori l'existence d'une base (finie) de .
.
1°)
2°)
3°)
Ces résultats, tu les connais ? C'est la clé des résultats que tu cites, en utilisant ce que tu dois savoir sur la dimension.
Edit : le 2 est un peu délicat, parce que tu ne peux pas supposer a priori l'existence d'une base (finie) de
Re: Théorèmes dimension
merci de vos réponses j'ai construit la preuve à l'aide des différentes indications que vous m'avez donné pourriez vous me dire si elle est correcte
Supposons F de dimension finie et f surjective
soit ( v1 , ..., vm ) une famille génératrice de E , Pour tout w de F , f(v) = w
v = a1 v1 + .. + am vm
w = f(a1 v1 + ... am vm) = a1f(v1) + ..+amf(vm)
Tout vecteur w de F est combinaison linéaire de la famille ( f(v1), ...? f(vm) ) qui est donc génératrice réciproquement si (f(v1),..., f(vm)) est génératrice alors un vecteur w de F s'écrit w= a1 f(v1)+ ... + am f(vm)
= f(a1 v1 + ...+ am vm)
donc w est l'image par f d'un vecteur de E , f est surjective et de dimension finie
d'après le théorème du rang dim E = dim ker f + dim im(f) or f est surjective donc dim im(f) = dim F donc si dim ker f = 0 dim F = dim E si dim ker f >= 1 dim E > dim F donc dim E >= dim F
Supposons F de dimension finie et f surjective
soit ( v1 , ..., vm ) une famille génératrice de E , Pour tout w de F , f(v) = w
v = a1 v1 + .. + am vm
w = f(a1 v1 + ... am vm) = a1f(v1) + ..+amf(vm)
Tout vecteur w de F est combinaison linéaire de la famille ( f(v1), ...? f(vm) ) qui est donc génératrice réciproquement si (f(v1),..., f(vm)) est génératrice alors un vecteur w de F s'écrit w= a1 f(v1)+ ... + am f(vm)
= f(a1 v1 + ...+ am vm)
donc w est l'image par f d'un vecteur de E , f est surjective et de dimension finie
d'après le théorème du rang dim E = dim ker f + dim im(f) or f est surjective donc dim im(f) = dim F donc si dim ker f = 0 dim F = dim E si dim ker f >= 1 dim E > dim F donc dim E >= dim F
Re: Théorèmes dimension
Pour tout w de F , f(v) = w
Tu oublies un bout de phrase : Pour tout w de F , il existe v dans E tel que f(v) = w (traduction de "f surjective").
Tu utilises ici la surjectivité de f (c'est l'hypothèse pour 1), et après tu fais comme si tu avais démontré cette surjectivité. Je ne comprends pas ta démarche.
Enfin, invoquer le théorème du rang ne me semble pas dans l'esprit de l'exercice.
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 83 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
