Bonjour, mes amis et moi avons un exercice d’équation différentielle à faire mais nous sommes bloqués dès le départ. Pouvez-vous nous aider ?
Voici le sujet :
Soit f une fonction continue sur R.
1. Déterminer, en fonction de f, la solution du problème de Cauchy suivant :
y’’ + y = f(x)
y(0)=y’(0)=0
2. Calculer la solution du système lorsque f(x)=cos(x).
Merci de votre aide.
Équation différentielle
12 messages
- Page 1 sur 1
Re: Équation différentielle
Bonsoir,
une piste : poser z(x) = y(x)exp(ix) et calculer z''(x) - 2iz'(x).
une piste : poser z(x) = y(x)exp(ix) et calculer z''(x) - 2iz'(x).
Re: Équation différentielle
Bonjour,
c'est une équation différentielle linéaire d'ordre 2 avec second membre.
Que dit le théorème du cours sur la structure de l'ensemble des solutions ?
Quelles sont les solutions de l'équation homogène?
Pour trouver une solution particulière, tu peux utiliser la méthode de variation des constantes pour l'ordre 2, mais c'est hors programme en CPGE.
c'est à dire un changement de fonction inconnue : on écrit y(x)=lambda(x)*z1(x)+mu(x)*z2(x)
où lambda et mu sont les fonctions inconnues
et z1 et z2 sont les solutions de l'équation homogène associée (on parle de système fondamental de solutions).
la piste de LA est une version de la méthode de variation de la constante (mais dans les complexes), pour la question 2.
EDIT : mon message original était hors sujet car valable pour les E.D. d'ordre 1.
c'est une équation différentielle linéaire d'ordre 2 avec second membre.
Que dit le théorème du cours sur la structure de l'ensemble des solutions ?
Quelles sont les solutions de l'équation homogène?
Pour trouver une solution particulière, tu peux utiliser la méthode de variation des constantes pour l'ordre 2, mais c'est hors programme en CPGE.
c'est à dire un changement de fonction inconnue : on écrit y(x)=lambda(x)*z1(x)+mu(x)*z2(x)
où lambda et mu sont les fonctions inconnues
et z1 et z2 sont les solutions de l'équation homogène associée (on parle de système fondamental de solutions).
la piste de LA est une version de la méthode de variation de la constante (mais dans les complexes), pour la question 2.
EDIT : mon message original était hors sujet car valable pour les E.D. d'ordre 1.
Modifié en dernier par LB2 le 11 Mar 2020, 12:06, modifié 2 fois.
Re: Équation différentielle
Bonsoir
Lorsqu'on connait la solution générale de l'équation homogène associée (c'est le cas ici, elle est à coefficients constants) il y a une autre méthode, souvent plus économes calculs :
https://fr.wikipedia.org/wiki/Méthode_de_variation_des_constantes
cas du second ordre
Bon courage
PS le lien ci dessus passe mal
https://fr.wikipedia.org/wiki/Méthode_de_variation_des_constantes
recopier cette adresse en entier, au besoin
Lorsqu'on connait la solution générale de l'équation homogène associée (c'est le cas ici, elle est à coefficients constants) il y a une autre méthode, souvent plus économes calculs :
https://fr.wikipedia.org/wiki/Méthode_de_variation_des_constantes
cas du second ordre
Bon courage
PS le lien ci dessus passe mal
https://fr.wikipedia.org/wiki/Méthode_de_variation_des_constantes
recopier cette adresse en entier, au besoin
Re: Équation différentielle
La variation des constantes plus économe en calculs que la variation de la constante? Je doute ^^
Re: Équation différentielle
La forme générale de la solution lorsque le second membre est général est assez difficile à obtenir avec la variation des constantes, version second ordre. Il est bon de connaitre la notion de wronskien pour cela.
Alternativement, on peut prendre la transformée de Laplace de cette équation différentielle pour montrer la formule suivante :
y = A cos(x) + B sin(x) + intégrale de 0 à x de (sin(x-t)f(t)dt)
Alternativement, on peut prendre la transformée de Laplace de cette équation différentielle pour montrer la formule suivante :
y = A cos(x) + B sin(x) + intégrale de 0 à x de (sin(x-t)f(t)dt)
Re: Équation différentielle
Bonjour,
Je pense que nous nous sommes mal compris : je ne préconisais pas spécialement l'emploi de la méthode de la variation des constantes pour trouver les solutions de l'équation homogène, mais je pense qu'elle est très performante pour trouver une solution de l'équation complète, dans le cas où on connaît déjà la solution générale de l'équation homogène.
C'est en particulier le cas lorsque les coefficients sont constants (e .d. linéaire d'ordre deux , homogène, à coefficients constants), donc c'est en particulier le cas ici.
Pour la transformée de Laplace c'est autre chose : est ce vu en cours ? Est ce attendu ici ?
Il faudrait que Charlottegbt en dise plus à ce sujet.
Une dernière remarque : si le but du 1 est de résoudre 2, c'est casser une noix avec un marteau-pilon : il existe des méthodes élémentaires beaucoup plus simples.
Bonne journée à tous
Je pense que nous nous sommes mal compris : je ne préconisais pas spécialement l'emploi de la méthode de la variation des constantes pour trouver les solutions de l'équation homogène, mais je pense qu'elle est très performante pour trouver une solution de l'équation complète, dans le cas où on connaît déjà la solution générale de l'équation homogène.
C'est en particulier le cas lorsque les coefficients sont constants (e .d. linéaire d'ordre deux , homogène, à coefficients constants), donc c'est en particulier le cas ici.
Pour la transformée de Laplace c'est autre chose : est ce vu en cours ? Est ce attendu ici ?
Il faudrait que Charlottegbt en dise plus à ce sujet.
Une dernière remarque : si le but du 1 est de résoudre 2, c'est casser une noix avec un marteau-pilon : il existe des méthodes élémentaires beaucoup plus simples.
Bonne journée à tous
Re: Équation différentielle
@Rdvn : nous disons la même chose à propos de la méthode de variation des constantes.
Je m'étonnais que tu dises que cette méthode était plus rapide qu'elle même.
Mon message d'origine était cependant hors sujet puisque j'évoquais la variation des constantes pour une E.D. du premier ordre.
Résumons nous donc :
Résoudre l'équation homogène y''+y = 0 ne pose aucune difficulté.
Il s'agit bien de trouver une solution particulière à l'équation y''+y = f(x)
où f(x) est un second membre quelconque.
Ainsi, la recherche de solutions particulières "sous une certaine forme" n'est pas possible.
Il reste donc uniquement la méthode générale de variation des constantes.
Sauf que : pour l'ordre 2, la méthode de variations des constantes n'est pas exigible en CPGE. Certains professeurs l'enseignent tout de même, on peut la voir par exemple ici : http://uel.unisciel.fr/physique/outils_ ... 10_03.html
Et effectivement, la question 2 est plus simple que la question 1 puisqu'on peut directement chercher une solution particulière sous la forme du second membre.
Je m'étonnais que tu dises que cette méthode était plus rapide qu'elle même.
Mon message d'origine était cependant hors sujet puisque j'évoquais la variation des constantes pour une E.D. du premier ordre.
Résumons nous donc :
Résoudre l'équation homogène y''+y = 0 ne pose aucune difficulté.
Il s'agit bien de trouver une solution particulière à l'équation y''+y = f(x)
où f(x) est un second membre quelconque.
Ainsi, la recherche de solutions particulières "sous une certaine forme" n'est pas possible.
Il reste donc uniquement la méthode générale de variation des constantes.
Sauf que : pour l'ordre 2, la méthode de variations des constantes n'est pas exigible en CPGE. Certains professeurs l'enseignent tout de même, on peut la voir par exemple ici : http://uel.unisciel.fr/physique/outils_ ... 10_03.html
Et effectivement, la question 2 est plus simple que la question 1 puisqu'on peut directement chercher une solution particulière sous la forme du second membre.
Re: Équation différentielle
Salut,
Un petit "truc" qui doit être compréhensible par un étudiant un peu dégourdi ayant fait de l'algèbre linéaire :
Quand on a une équation différentielle linéaire d'ordre 2 (voire de n'importe quel ordre >1) comme par exemple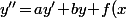) (E), on peut en fait la voir comme une équa-diff. d'ordre 1, mais avec des vecteurs :
(E), on peut en fait la voir comme une équa-diff. d'ordre 1, mais avec des vecteurs :
Si on pose alors on a
alors on a  et l'équation (E) peut s'écrire
et l'équation (E) peut s'écrire \end{pmatrix}) (Ev).
(Ev).
Ensuite, on sait que les solutions de l'équation homogène associée sont de la forme
sont de la forme  où
où  et
et  sont deux constantes arbitraires ce qui signifie que
sont deux constantes arbitraires ce qui signifie que  et c'est sous cette forme là qu'on utilise la méthode de variation de la constante en écrivant
et c'est sous cette forme là qu'on utilise la méthode de variation de la constante en écrivant  (*) où
(*) où  et
et  sont deux fonctions. Et quand on injecte ça dans (Ev), ça va bien sûr donner DEUX équations concernant
sont deux fonctions. Et quand on injecte ça dans (Ev), ça va bien sûr donner DEUX équations concernant  et
et  et pas une seule.
et pas une seule.
Et on peut facilement retrouver quelle est cette deuxième équation en constatant que (*) dit non seulement que , mais aussi que
, mais aussi que  ce qui signifie aussi (en regardant dérivée de la première relation) que
ce qui signifie aussi (en regardant dérivée de la première relation) que  .
.
En bref, en prenant comme tu le fait uniquement l'équation bleue et aucune des deux équations (équivalentes) en rouge pour ta méthode de "variation de la constante", ben je pense pas que tu arrivera à grand chose.
Si tu n'écrit "que ça", c'est plutôt mal barré vu que tu va avoir deux inconnues (lambda et mu) pour une seule équation (l'équation différentielle de départ).LB2 a écrit:...c'est à dire un changement de fonction inconnue : on écrit y(x)=lambda(x)*z1(x)+mu(x)*z2(x)
où lambda et mu sont les fonctions inconnues
et z1 et z2 sont les solutions de l'équation homogène associée (on parle de système fondamental de solutions).
Un petit "truc" qui doit être compréhensible par un étudiant un peu dégourdi ayant fait de l'algèbre linéaire :
Quand on a une équation différentielle linéaire d'ordre 2 (voire de n'importe quel ordre >1) comme par exemple
Si on pose
Ensuite, on sait que les solutions de l'équation homogène associée
Et on peut facilement retrouver quelle est cette deuxième équation en constatant que (*) dit non seulement que
En bref, en prenant comme tu le fait uniquement l'équation bleue et aucune des deux équations (équivalentes) en rouge pour ta méthode de "variation de la constante", ben je pense pas que tu arrivera à grand chose.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Équation différentielle
Oui tout à fait, il faut ajouter la contrainte lambda'(x)z1(x)+mu'(x)z2(x) = 0 avec mes notations
Je me demandais d'où venait cette contrainte et je ne voyais pas de façon de la justifier autrement que la méthode de Ben (toute équation différentielle linéaire scalaire d'ordre n se ramène à l'ordre 1 sur un espace plus grand). J'ai un vague souvenir d'une approche différente (en restant scalaire) avec le wronskien mais c'est trop flou.
Cette méthode aboutit à une solution en lambda' et mu', exprimés en fonction de f, puis à une expression intégrale pour la solution particulière.
Question :
La résolution du système différentiel linéaire d'ordre 1 en lambda et mu est-elle possible pour n'importe quelle E.D. linéaire d'ordre 2 au départ ? (et pas juste y''+y = f(x) ).
Car ma solution utilise cos^2(x)+sin^2(x) = 1
Je me demandais d'où venait cette contrainte et je ne voyais pas de façon de la justifier autrement que la méthode de Ben (toute équation différentielle linéaire scalaire d'ordre n se ramène à l'ordre 1 sur un espace plus grand). J'ai un vague souvenir d'une approche différente (en restant scalaire) avec le wronskien mais c'est trop flou.
Cette méthode aboutit à une solution en lambda' et mu', exprimés en fonction de f, puis à une expression intégrale pour la solution particulière.
Question :
La résolution du système différentiel linéaire d'ordre 1 en lambda et mu est-elle possible pour n'importe quelle E.D. linéaire d'ordre 2 au départ ? (et pas juste y''+y = f(x) ).
Car ma solution utilise cos^2(x)+sin^2(x) = 1
12 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 42 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
