Bonjour ,
Je m'intéresse à la preuve du théorème suivant : l'exponentielle réalise une bijection entre les matrices nilpotentes et les matrices unipotentes.
Dans mon livre ,on utilise un développement en série entière de ln(In +N)
Peut-on toujours effectuer un développement en série entière quelque soit la matrice N? ll ne manque pas une condition sur la norme matricielle de N? N'est ce pas vrai uniquement si norme de N est inférieure à 1??
On utilise ensuite un développement limité et j'ai du mal à comprendre...
Merci
EXPONENTIELLE DE MATRICE
7 messages
- Page 1 sur 1
Re: EXPONENTIELLE DE MATRICE
Bonsoir,
je dis peut-être une bêtise, mais si N est nilpotente, la série entière est une somme finie donc converge.
[edit] et pour le développement limité c'est peut-être une histoire de théorème d'inversion locale.
je dis peut-être une bêtise, mais si N est nilpotente, la série entière est une somme finie donc converge.
[edit] et pour le développement limité c'est peut-être une histoire de théorème d'inversion locale.
Re: EXPONENTIELLE DE MATRICE
En fait alibabadu59, on peut se contenter d'utiliser une série formelle pour cette preuve et non une série entière, pour se débarasser des problèmes de convergence. Mais utiliser les séries entières et imposer une condition sur la norme de N fonctionne également. Je rappelle que la série entière de ln(1+x) a pour rayon de convergence 1. Quel est le point qui te pose problème précisément?
Re: EXPONENTIELLE DE MATRICE
Ok merci beaucoup !
Ce qui me pose problème c'est l'utilisation d'un développement limité avec des matrices... Il y a aucune condition à vérifier avant d'effectuer ce genre de DL? Merci
Ce qui me pose problème c'est l'utilisation d'un développement limité avec des matrices... Il y a aucune condition à vérifier avant d'effectuer ce genre de DL? Merci
Re: EXPONENTIELLE DE MATRICE
Je rappelle que l'exponentielle d'une matrice nilpotente est une somme finie.
Si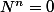 alors un DL à l'ordre
alors un DL à l'ordre  suffit pour avoir l'exponentielle de
suffit pour avoir l'exponentielle de  (les autres termes de la série étant nuls).
(les autres termes de la série étant nuls).
Si
Re: EXPONENTIELLE DE MATRICE
oui oui.
Mais il y a vraiment une histoire de théorème d'inversion locale ici? merci
Mais il y a vraiment une histoire de théorème d'inversion locale ici? merci
Re: EXPONENTIELLE DE MATRICE
Je ne pense pas cela reste un problème d'algèbre, avec
=I+N+N^2/2+...+N^{n-1}/(n-1)!)
et la fonction
=(A-I)-(A-I)^2/2+...+(-1)^{n+1}(A-I)^{n-1}/(n-1)) est la fonction réciproque.
est la fonction réciproque.
lorsque l'on travaille avec des matrices tel que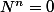
et la fonction
lorsque l'on travaille avec des matrices tel que
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 67 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
