Bonjour,
Soit (G, *) un groupe quelconque et "e" son élément neutre. Supposons que pour tout g dans G, g² = g*g = e.
Soit x et y appartenant a G.
Il faut que je calcule (x*y)^(-1),
Que je montre que x = x^-1
Et que, finalement, je dois en deduire que (G, *) est commutatif.
Ca fait plusieurs jours que je n'arrive pas a aborder une rédaction correcte face a ces questions, ni meme un raisonnement rationnel. Pouvez-vous me mettre sur la piste ?
Groupes et loi (Algèbre linéaire)
4 messages
- Page 1 sur 1
Re: Groupes et loi (Algèbre linéaire)
Salut !
1. En considérant^2) , montre que
, montre que ^{-1}=xy) .
.
2. Que se passe-t-il pour ?
?
3. De façon générale^{-1}=y^{-1} x^{-1}) donc à l'aide de la question précédente, déduis-en que
donc à l'aide de la question précédente, déduis-en que 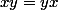 .
.
1. En considérant
2. Que se passe-t-il pour
3. De façon générale
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Re: Groupes et loi (Algèbre linéaire)
capitaine nuggets a écrit:Salut !
1. En considérant, montre que
.
2. Que se passe-t-il pour?
3. De façon généraledonc à l'aide de la question précédente, déduis-en que
.
Merci pour votre réponse rapide !
Cependant, est-il possible de calculer xy^-1 sans pour autant avoir connaissance que x² = e ?
Re: Groupes et loi (Algèbre linéaire)
En général, dans un groupe, (xy)^(-1) = (y)^(-1) * (x)^(-1)
Sans savoir que tout élément est son propre inverse, on ne peut pas continuer ce raisonnement.
Pour prolonger ton exercice, avec une difficulté croissante, tu as :
- même question si on suppose (ab)^2 = a^2 b^2 pour tous éléments a,b
- même question si on suppose (ab)^3 = a^3 b^3 pour tous éléments a,b, et G n'admet aucun élément d'ordre 3 (c'est à dire x^3 = e => x = e)
Sans savoir que tout élément est son propre inverse, on ne peut pas continuer ce raisonnement.
Pour prolonger ton exercice, avec une difficulté croissante, tu as :
- même question si on suppose (ab)^2 = a^2 b^2 pour tous éléments a,b
- même question si on suppose (ab)^3 = a^3 b^3 pour tous éléments a,b, et G n'admet aucun élément d'ordre 3 (c'est à dire x^3 = e => x = e)
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 45 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
