J’ai un DM à rendre pour la rentré mais une seul question me pose problème voici l’énoncé jusqu’à celle-ci. Heureusement cette question est indépendantes des autres question du DM. Si vous voulez des précisions sur la suite du DM dite le moi.
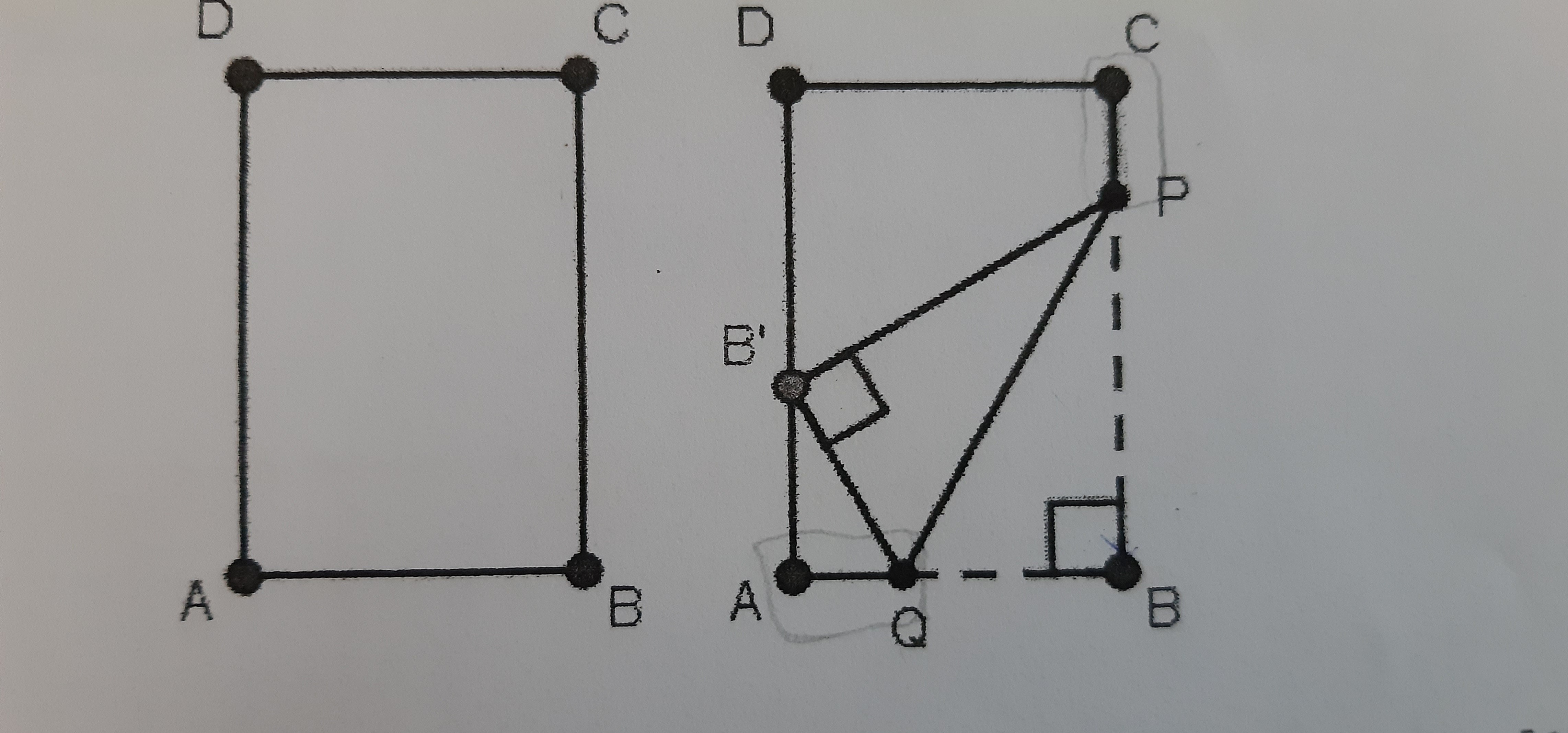
On dispose d’une feuille de papier A4 de format 21X29,7 représenter par le rectangle ABCD ci-dessous. On plie cette feuille de façon à amener le point B en B’ sur le segment[AD] et Q sur [AB], ou [QP) représente la demie-droite de pliage, avec p appartient [BC). Le but du problème est de déterminer la longueur minimale de QP du pliage, ainsi que la où les positions du pont B’ rendant cette longueur minimale.
 Sur l'image la longueur y est une erreur
Sur l'image la longueur y est une erreur1) Réaliser sur Geogebra un figure à l’échelle 1/2 en prenant le point Q mobile sur [AB].
Conjecture alors un encadrement des longueurs AB’et QP répondant au problème .
2) On choisit BQ comme variable et on pose BQ=x
-Dans quel intervalle I doit se situer x pour que le point B’ soit bien définie. Justifier
Donc bien-sur c’est la question 2 qui me pose problème ainsi je trouve l’intervalle suivant
x € ]10,5;21] (sans géogébra) et avec géogébra x € [12,3;21].
Si dans le premier intervalle on ne prend pas 10,5 c est parce que plus tard dans le dm c’est une valeur interdite.
La justification pour cette question m’est impossible à trouver sauf pour 21 car si x dépasse 21 le point Q n’appartient plus à [AD].
J’ai besoin juste de cette question pour finir.
Merci d’avance de votre aide