Limite suite produit

[hello213]

Bonjour !

Je dois déterminer la limite d'une suite définie par un produit
_____2n-1
Un = ∏ (2 - (k/2n))
_____k=1

Dois-je procéder par encadrement?
Si quelqu'un pouvait juste m'aider à démarrer ce serait gentil!

Merci et bonne journée à vous

[GaBuZoMeu]

Je prendrais le logarithme, et je me dirais "hum hum, ça sent la somme de Riemann".

Au fait, n'as-tu pas oublié un petit exposant ? Parce que tel quel, la réponse est assez évidente.

[hello213]

merci pour votre réponse !
et non je n'ai pas oublié d'exposant

[GaBuZoMeu]

Je répète : avec le tel que tu l'as écrit, la question est assez triviale (la moitié des facteurs est supérieure ou égale à 3/2).
Pour , ça devient déjà plus intéressant.

[hello213]

.

[hello213]

(la moitié des facteurs est supérieure ou égale à 3/2).

d'accord, mais pour l'instant je ne vois pas trop pour la suite...

[GaBuZoMeu]

Quelle suite ? Ne vois tu pas une minoration évidente qui montre que le produit tend vers avec ?

[hello213]

ai-je le droit de minorer par 2n ? ainsi 2n tend vers + l'infini donc le produit tend bien vers + l'infini?

[GaBuZoMeu]

La question n'est pas d'"avoir le droit", la question est de démontrer une minoration. Si tu sais démontrer que est minoré par , fais-le !
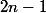
Personnellement, ce n'est pas la minoration que j'ai en vue et vers laquelle je pensais t'aiguiller en signalant que la moitié des facteurs dans (très exactement, facteurs sur les ) est supérieure ou égale à 3/2.

[hello213]

oui, et justement c'est pour après que je bloque, car pour les autres facteurs...

désolé, c'est censé être évident mais je mets du temps à comprendre ahah!

[GaBuZoMeu]

car pour les autres facteurs

Ne vois-tu pas qu'ils sont tous supérieurs ou égaux à 1 ? Même après ce que tu as écrit sur les-mathématiques.net ?

[hello213]

oui je vois
mais il faut bien que le minorant tende vers + l'infini ?

[GaBuZoMeu]

Voyons ... Un produit de nombres tous supérieurs ou égaux à 1 et dont d'entre eux sont supérieurs ou égaux à 3/2. Dur dur de trouver un minorant qui tend vers avec ???

[hello213]

c'est bon!
En tout cas merci beaucoup pour votre aide