Bonjour,
J’ai un DM de maths spé à rendre, et je bloque sur la dernière question d’un exercice.
Voici l’énoncé :
1) soit P, un nombre premier. Soit x appartient à Z. Soit d = pgcd(p;x). Montrez que d=1 et d=p.
2) en déduire que soit pgcd(p;x)=1, soir p divise x
3) Soit x un entier non divisible par p. Montrer alors qu’il existe au moins un entier u tel que xu=1(mod p)
4) montrez qu’il existe un unique entier x’ compris entre 1 et p-1 tel que xx’=1(mod p). (On cherche ici à montrer l’unicite)
5) Déterminer les entiers x compris entre 1 et p-1 tels que x’=x
Je pense avoir la solution des 4 premières questions mais je n’arrive pas à la 5...
Je pense que je ne comprends pas ce que l’on nous demande... on ne peut pas énoncer les cas particuliers (il y a une infinité de nombres premiers) donc on nous demande l’expression de x en fonction de p ? Dans ce cas, si xx’=1(mod 1) alors x^2=1(mod1) alors x = racine(kp+1)
Mais 1<kp+1<(p-1)^2
Donc 0<k<p-2
Je ne sais pas du tout si je suis sur la bonne voix ou pas du tout...
Merci d’avance pour vos réponses.
Maths spé, nombres premiers
5 messages
- Page 1 sur 1
Re: Maths spé, nombres premiers
Si 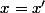 alors
alors  donc
donc  puis
puis (x+1)\equiv 0[p]) . Comme
. Comme  est premier,
est premier,  ou
ou  . Comme
. Comme  , on a
, on a  ou
ou 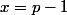 . Si réciproquement
. Si réciproquement  ou
ou 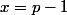 , alors je te laisse vérifier que
, alors je te laisse vérifier que  et comme
et comme  par unicité
par unicité 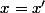 .
.
Re: Maths spé, nombres premiers
Bonjour,
Merci pour votre réponse. Je pense avoir compris la démarche, cependant j’ai une petite question. Pourquoi comme p est premier, il divise soit x-1 soit x+1 ? Je ne vois pas le lien avec le fait qu’il soit premier...
Merci.
Merci pour votre réponse. Je pense avoir compris la démarche, cependant j’ai une petite question. Pourquoi comme p est premier, il divise soit x-1 soit x+1 ? Je ne vois pas le lien avec le fait qu’il soit premier...
Merci.
Re: Maths spé, nombres premiers
Il s'agit du lemme d'Euclide : si  est un nombre premier tel que
est un nombre premier tel que  alors
alors  ou
ou  . Il se déduit du lemme de Gauss : si
. Il se déduit du lemme de Gauss : si  alors c'est fini, si
alors c'est fini, si  ne divise pas
ne divise pas  alors
alors  et
et  sont premiers entre eux (si
sont premiers entre eux (si  est le pgcd de
est le pgcd de  et
et  alors
alors  et
et  étant premier, on a
étant premier, on a 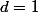 ou
ou 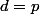 . Comme de plus
. Comme de plus 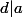 , alors
, alors  donc
donc 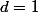 ). En résumé
). En résumé  et
et  et
et  sont premiers entre eux, d'après le lemme de Gauss
sont premiers entre eux, d'après le lemme de Gauss  .
.
Re: Maths spé, nombres premiers
D’accord merci.
Comme la lemme d’Euclide ne figure pas dans mon cours si je précise juste que si un nombre premier divise un produit de deux nombres alors il divise l’un de ces deux nombres, est-ce suffisant ?
Merci pour votre réponse et votre temps.
Comme la lemme d’Euclide ne figure pas dans mon cours si je précise juste que si un nombre premier divise un produit de deux nombres alors il divise l’un de ces deux nombres, est-ce suffisant ?
Merci pour votre réponse et votre temps.
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 114 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
