Bonjour,
Je dois répondre à la question suivante:
À l'aide des sommes de Riemann, trouver une estimation en utilisant 8 sous intervalles et la borne de gauche de chaque sous intervalles.
La fonction est f(x)= 8x^2
Sur l'intervalle [1,3]
Est-ce que quelqu'un pourrais m'aider, car je n'arrive pas à la bonne réponse qui est 61,5
Merci
Calcul Intégral (sommes de Riemann)
9 messages
- Page 1 sur 1
Re: Calcul Intégral (sommes de Riemann)
Salut,
Eh bien tu traces 8 rectangles de largeur égale, c'est-à-dire 1/4 et tu sommes les valeurs à gauche, c'est-à-dire :
8.1²+8.(5/4)²+...+8.(11/4)²
Eh bien tu traces 8 rectangles de largeur égale, c'est-à-dire 1/4 et tu sommes les valeurs à gauche, c'est-à-dire :
8.1²+8.(5/4)²+...+8.(11/4)²
Re: Calcul Intégral (sommes de Riemann)
Parfait merci! Mais est-ce qu'il a une façon d'aller plus rapidement à la réponse?
Merci
Merci
Calcul intégral
Bonjour,
Je n'arrive pas à résoudre la sommation suivante à l'aide des propriétés. Est-ce que quelqu'un pourrais m'aider svp?
Merci
{\sum_{k=0}^{7}{8(\frac{k+4}{4})^2\frac{1}{4}}}
Je n'arrive pas à résoudre la sommation suivante à l'aide des propriétés. Est-ce que quelqu'un pourrais m'aider svp?
Merci
{\sum_{k=0}^{7}{8(\frac{k+4}{4})^2\frac{1}{4}}}
Re: Calcul intégral
C'est la suite de l'exercice de l'autre fil. Pourquoi ne pas continuer dans ce fil ?
Tu as huit termes à calculer, et ensuite à faire leur somme.
Pas très marrant, mais pas insurmontable. Tu peux le faire.
Tu as huit termes à calculer, et ensuite à faire leur somme.
Pas très marrant, mais pas insurmontable. Tu peux le faire.
Re: Calcul Intégral (sommes de Riemann)
@ megan message 20h09
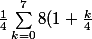^2=\frac{8}{4}\sum_{k=0}^7(\frac{4+k}{4})^2=\frac{2}{16}\sum_{k=0}^7(4+k)^2)
On a une formule pour la somme des carrés de 1 à n .
On a une formule pour la somme des carrés de 1 à n .
Re: Calcul Intégral (sommes de Riemann)
Sans formule, 16+25+36+49+64+81+100+121, ce n'est tout de même pas la mer à boire !
Modifié en dernier par GaBuZoMeu le 06 Fév 2020, 13:56, modifié 1 fois.
Re: Calcul Intégral (sommes de Riemann)
Merci à toi . megan pourra donc constater que ta réponse est la plus courte ... sans oublier que si le pas venait à diminuer , il serait plus pratique d'utiliser la formule .
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 38 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
