Nombres inconnus : x, y et z

[Formula2002]

Bonjour à tous et à toutes,

Voici ci-joint un exercice que je n'arrive pas à débuter. Serait-il possible de m'aider à démarrer cet exercice en me donnant quelques pistes?

Merci d'avance,
Cordialement

[MrPropre]

Je n'ai pas la réponse mais:
Admettons que x=1 donc:

yz>1 --> nécessairement z > 1 (ou y > 1) --> y> 1/z
1+ y + z < 1 + 1/y + 1/z <=> y + z < 1/y + 1/z

après je sais pas

[nodgim]

Ce serait que le sujet soit recopié, parce que là.......

[mathelot]

bonsoir,
pour la question 1, remplace z par 1 et obtiens une inégalité impossible,i.e, sans solutions.


pour la question 2, rajoute au système de deux (en fait de cinq inéquations ) inéquations les inégalités
et obtiens une inégalité impossible.

[Formula2002]

En remplaçant z par 1 dans la première équation, j'obtiens xy> 1 et dans la deuxième, x+ y+1<y + 1 + y/x

ce qui revient à x^2 < y
et à ce moment je ne sais pas vraiment à quoi tout cela me mène.. je suis bloqué sur la question 1

[mathelot]

pour la question 1
on remplace z par 1, il vient:

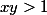
et
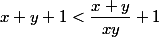
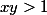
et
on simplifie par x+y, il vient:

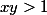
et
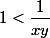
soit
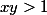
et
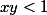
impossible

La question 2 se traite de façon similaire.