bonjour
voici la question qui a rapport avec les complexes on se demande d'indiquer dans le plan complexe l'ensemble des points M tels que l'imaginaire de (z+1)² = 2*réel de z
avec z est l'affixe de M
merci pour votre aide
Les nombres complexes
9 messages
- Page 1 sur 1
Re: les nombres complexes
Bonjour
On peut toujours commencer par poser z=x+iy , où x et y sont deux réels quelconques.
Ainsi Re(z) = x
Et
z+1 = x+1+iy , on peut facilement présenter (z+1)^2 sous forme X+iY , où X et Y sont des réels.
Proposez un premier essai
Bon courage
On peut toujours commencer par poser z=x+iy , où x et y sont deux réels quelconques.
Ainsi Re(z) = x
Et
z+1 = x+1+iy , on peut facilement présenter (z+1)^2 sous forme X+iY , où X et Y sont des réels.
Proposez un premier essai
Bon courage
Re: les nombres complexes
bonjour Rdvn j'ai déjà essayé mais je tombe dans cette equation y+x.y-2.x=0 quelle est ni une équation d'une droite ni d'un cercle!
Re: les nombres complexes
Bonsoir,
Sa Majesté vous a déjà donné la bonne réponse , vous avez oublié de simplifier par 2 :
(a+bi)^2 = a^2 +(bi)^2+2.a.bi=a^2-b^2+2abi
à appliquer à z^2.
Après cela, ce n'est ni une droite ni un cercle : il faut tracer la courbe d'équation y=x/(x+1) en faisant une étude de fonction (c'est une hyperbole, mais je ne suis pas sûr que ceci soit au programme en terminale).
Bon courage
Sa Majesté vous a déjà donné la bonne réponse , vous avez oublié de simplifier par 2 :
(a+bi)^2 = a^2 +(bi)^2+2.a.bi=a^2-b^2+2abi
à appliquer à z^2.
Après cela, ce n'est ni une droite ni un cercle : il faut tracer la courbe d'équation y=x/(x+1) en faisant une étude de fonction (c'est une hyperbole, mais je ne suis pas sûr que ceci soit au programme en terminale).
Bon courage
Re: les nombres complexes
Salut !
Nul besoin de connaître la nature des coniques obtenues, l'indication de Rdvn suffit largement.
En posant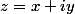 , on a
, on a
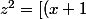+iy]^2 = (x+1)^2+2iy(x+1) + (iy)^2 =x^2+2x+1 -y^2+2iy(x+1)) ,
,
donc résoudre^2 = 2 {\rm Re}(z)) revient à résoudre
revient à résoudre  = 0) , c'est-à-dire
, c'est-à-dire
=0 }<br />\end{cases})
Enfin, sachant que la deuxième équation est ne équation produit-nul, ce système équivaut à
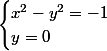 ou
ou 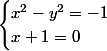

Nul besoin de connaître la nature des coniques obtenues, l'indication de Rdvn suffit largement.
Rdvn a écrit:Bonjour
On peut toujours commencer par poser z=x+iy , où x et y sont deux réels quelconques.
Ainsi Re(z) = x
Et
z+1 = x+1+iy , on peut facilement présenter (z+1)^2 sous forme X+iY , où X et Y sont des réels.
Proposez un premier essai
Bon courage
semowho a écrit:bonjour Rdvn j'ai déjà essayé mais je tombe dans cette equation y+x.y-2.x=0 quelle est ni une équation d'une droite ni d'un cercle!
En posant
donc résoudre
Enfin, sachant que la deuxième équation est ne équation produit-nul, ce système équivaut à
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Re: les nombres complexes
@capitaine nuggets : ce que tu racontes ne va pas du tout. Tu as oublié que ce n'est pas ^2) dans l'équation, mais sa partie imaginaire !
dans l'équation, mais sa partie imaginaire !
Re: les nombres complexes
Mea culpa, j'ai lu trop vite 
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 59 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
