As-tu compris les points suivants :
1°) À chaque permutation

de

correspond un événement
} < \ldots<X_{\sigma(n)})
et sur un tel événement la valeur de la suite
)
est fixée.
2°) Étant donné une des
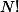
valeurs possibles de la suite
)
, on peut reconstruire l'ordre dans lequel sont les variables
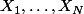
, c.-à-d. qu'on peut reconstituer la permutation

.
3°) Les événements

sont équiprobables.
4°) Les
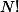
valeurs possibles de la suite
)
sont donc équiprobables.
5°) De là suit le fait que les
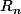
sont indépendantes.
PS. La suite
)
prend ses valeurs dans

. Par exemple la valeur (1,1,3,2,3,5) donne la permutation (3,6,1,5,4,2). Étape par étape :
(1) donne (1)
(1,1) donne (1,2)
(1,1,3) donne (3,1,2)
(1,1,3,2) donne (3,1,4,2)
(1,1,3,2,3) donne ((3,1,5,4,2)
PPS. Tu peux voir le paragraphe "Loi uniforme sur un produit cartésien" dans
la page wikpedia sur l'indépendance.PPPS. @Ben314 :
Si on prend

, le fait que
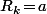
signifie que
\!=\!k)
(avec tes notations),
Non, ce n'est pas ça comme tu peux le voir sur l'exemple en PS.
