Résolution équation
19 messages
- Page 1 sur 1
Résolution équation
Bonjour j'ai un exercice de maths et je bloque à une question j'ai essayé de résoudre mais je n'arrive Pas à tomber sur un polynôme
L'équation est sh(x) /x=(n+1)/n et la question est
Montrer que pour tout n appartient à N.etoile l'équation admet deux solutions dont une strictement positive
merci d'avance
L'équation est sh(x) /x=(n+1)/n et la question est
Montrer que pour tout n appartient à N.etoile l'équation admet deux solutions dont une strictement positive
merci d'avance
Re: Résolution équation
bonjour,
étudie les variations de/x) sur
sur 
i) la fonction est elle paire, impaire ou rien du tout ?
ii) que se passe-t-il pour x=0 ?
iii) une fois le tableau de variations dressé , applique le TVI (théorème des valeurs intermédiaires
remarque (n+1)/n = 1+1/n
la quantité 1+1/n est bornée par quelles valeurs ?
étudie les variations de
i) la fonction est elle paire, impaire ou rien du tout ?
ii) que se passe-t-il pour x=0 ?
iii) une fois le tableau de variations dressé , applique le TVI (théorème des valeurs intermédiaires
remarque (n+1)/n = 1+1/n
la quantité 1+1/n est bornée par quelles valeurs ?
Re: Résolution équation
Oui ça c'était les questions d'avant et j'ai trouvé qu'elle était pair, proongeable en une fonction continue sur R et strictement croissante sur R mais je vois pas le rapport avec cette question
Re: Résolution équation
Par contre après il faut montrer que la. Suite xn est décroissante en prenant xn la solution positive de l'équation et il est marqué qu'il faut raisonner par l'absurde je galère ici
Re: Résolution équation
en démonstration directe:
Pour tout entier n strictement positif,
}{x_n}=1+\dfrac{1}{n})
}{x_{n+1}}=1+\dfrac{1}{n+1})
d'où
}{x_{n+1}} <\dfrac{sh(x_n)}{x_n})
la fonction}{x}) étant strictement croissante sur
étant strictement croissante sur 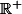

Cette démo directe se convertit facilement en "raisonnement par l'absurde"
Pour tout entier n strictement positif,
d'où
la fonction
Cette démo directe se convertit facilement en "raisonnement par l'absurde"
Re: Résolution équation
OK ça marche j'avais fait un truc similaire mais après faut montrer qu'elle converge mais faut partir de ce résultat ducoup ?
Re: Résolution équation
oui.
Quelle propriété la suite ) possède-t-elle en plus d'être strictement décroissante ?
) possède-t-elle en plus d'être strictement décroissante ?
Quelle propriété la suite
Re: Résolution équation
on fait tendre n vers l'infini.
f est une bijection croissante de [0;+oo[ sur [1;+oo[ , continue.
elle admet une bijection réciproque g.
que vaut g(1) ?
Re: Résolution équation
on n'a pas de formule close pour exprimer g(y).
par contre comme f(0)=1 , que vaut g(1) ?
par contre comme f(0)=1 , que vaut g(1) ?
19 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 57 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
